1 Informer

论文名称：Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
论文地址：https://arxiv.org/abs/2012.07436 (opens new window)
引用量（截止到2025.07.08）：6171
Venue：AAAI 2021
GitHub：https://github.com/zhouhaoyi/Informer2020 (opens new window)
Star：6000+

2 一句话总结这篇论文

这篇论文提出了 ProbSparse 自注意力机制（[其实就是挑选 top-k 个query，详细见6.2](#6.2 查询稀疏性度量)），自注意力蒸馏操作（加了卷积进去加了卷积进去，详细见6.5）。

3 摘要

摘要：许多现实世界的应用需要对长序列时间序列进行预测，例如电力消耗规划。长序列时间序列预测（LSTF）对模型的预测能力提出了较高要求，即高效捕捉输入与输出之间精确的长距离依赖关系。近年来的研究表明，Transformer在提升预测能力方面具有潜力。然而，Transformer存在几个严重问题，限制了其在LSTF中的直接应用，包括二次时间复杂度、高内存消耗以及编码器-解码器架构的固有限制。为了解决这些问题，我们设计了一种用于LSTF的高效Transformer模型，命名为Informer，具有以下三个显著特点：

• 提出ProbSparse自注意力机制，在时间和内存开销上实现O(L log L)的复杂度，同时在序列依赖对齐方面具有可比性能；
• 提出自注意力蒸馏操作，通过层间输入减半来突出主导注意力，从而高效处理极长的输入序列；
• 设计生成式解码器，以一次前向传播的方式预测长时间序列，而非逐步生成，显著提升长序列预测的推理速度。

在四个大规模数据集上的广泛实验证明，Informer在性能上显著优于现有方法，为LSTF问题提供了一种全新的解决方案。

4 引言

时间序列预测在许多领域中都至关重要，例如传感器网络监控、能源与智能电网管理、经济与金融、疾病传播分析等。在这些场景中，我们可以利用大量历史时间序列数据进行长期预测，即长序列时间序列预测（LSTF）。然而，现有方法大多是为短期预测问题设计的，例如预测48个时间点或更少。当序列变得越来越长时，模型的预测能力会受到极大考验，导致LSTF研究进展受限。

一个实际示例如图1所示：LSTM模型对某电力变压器站点的小时温度进行预测，从短期（12个点，即0.5天）到长期（480个点，即20天）。当预测长度超过48个点时（图1b中的实心星标所示），模型性能显著下降，MSE急剧上升，推理速度骤降，LSTM模型开始失效。

长序列时间序列预测（LSTF）面临的主要挑战是提升预测能力，以满足对越来越长的序列的需求，这要求模型具备：(a) 出色的长距离依赖对齐能力，以及 (b) 高效处理长序列输入与输出的能力。近年来，Transformer模型在捕捉长距离依赖方面表现优于RNN模型。其自注意力机制可以将网络信号传播路径缩短至理论上的最短O(1)，并避免使用循环结构，因此在LSTF问题中展现出巨大潜力。

然而，自注意力机制违背了第(b)点的高效性要求，因为它在处理长度为L的输入/输出时，计算与内存消耗为二次复杂度O(L²)。一些大规模的Transformer模型虽然在自然语言处理任务中取得了令人瞩目的成果，但其依赖于数十张GPU的大规模训练与高昂的部署成本，使得它们难以应用于真实场景中的LSTF问题。因此，自注意力机制与Transformer架构的效率问题，成为其在LSTF应用中的瓶颈。

为此，本文旨在探讨：我们是否可以改进Transformer模型，使其在计算、内存和架构方面更高效，同时仍然保持强大的预测能力？

原始Transformer在处理LSTF问题时存在以下三大主要限制：

1. 自注意力机制的二次计算复杂度。其基本操作——标准点积注意力——导致每一层的时间与内存复杂度为O(L²)。
2. 长序列输入下的内存瓶颈。J层的编码器/解码器堆叠导致总内存消耗为O(J·L²)，限制了模型接收长序列输入的扩展性。
3. 预测长序列时推理速度急剧下降。原始Transformer的动态解码方式使其逐步生成过程与RNN模型一样缓慢（如图1b所示）。

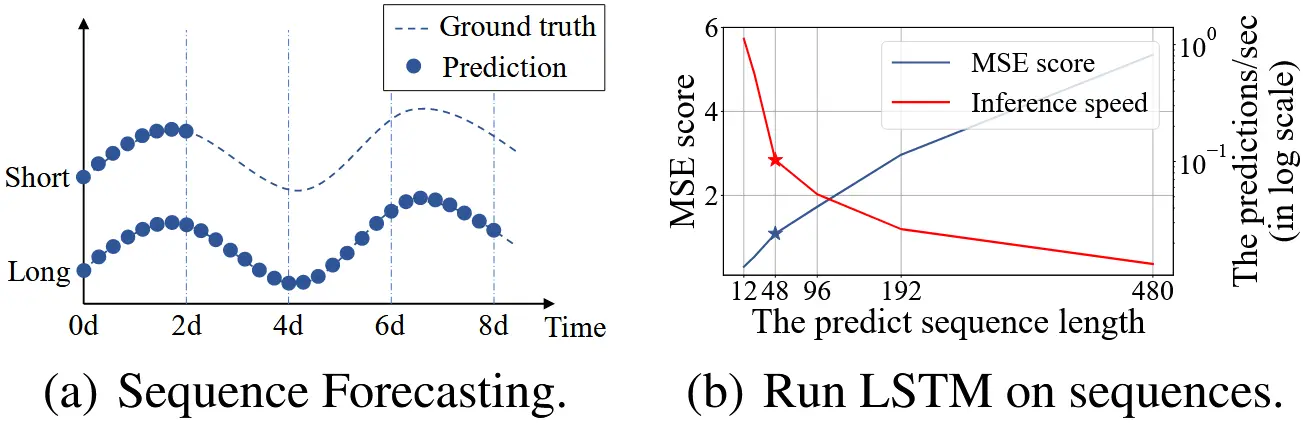图 1 说明：(a) 长序列时间序列预测（LSTF）相较于短序列预测，可覆盖更长时间跨度，在政策规划与投资决策保护等场景中具有重要意义。 (b) 现有方法的预测能力严重限制了 LSTF 的性能。例如，从预测长度达到 48 开始，均方误差（MSE）迅速上升至不可接受的水平，同时推理速度急剧下降，模型难以胜任更长预测任务。

已有一些研究致力于提高自注意力机制的效率。例如，Sparse Transformer、LogSparse Transformer 和 Longformer 都采用启发式方法来应对第1个限制（即计算复杂度问题），将自注意力机制的复杂度降至 O(L log L)，但这些方法的效率提升仍然有限。Reformer 也实现了 O(L log L) 的复杂度，使用的是局部敏感哈希注意力机制，但它仅适用于极长的序列。Linformer 最近提出了理论上的线性复杂度 O(L)，但其投影矩阵在真实世界的长序列输入中难以固定，存在退化为 O(L²) 的风险。

Transformer-XL 和 Compressive Transformer 试图引入辅助隐藏状态来捕捉长距离依赖，但反而可能加剧第1个限制，并不利于突破效率瓶颈。这些方法多数仅解决了第1个限制，而限制2与限制3在LSTF问题中仍未得到解决。

为此，我们提出 Informer，从根本上解决上述所有限制，不仅提升了效率，还增强了模型的预测能力。我们专注于这三个问题，探索了自注意力机制中的稀疏性，对网络组件进行了改进，并开展了大量实验验证。本文的贡献总结如下：

• 我们提出了Informer模型，成功增强了LSTF问题中的预测能力，验证了Transformer类模型在捕捉长序列输入输出之间的个体化长距离依赖关系方面的潜力。
• 我们设计了ProbSparse自注意力机制，高效替代传统的全连接自注意力，在依赖对齐上实现了 O(L log L) 的时间复杂度与内存复杂度。
• 我们提出了自注意力蒸馏操作，通过在多层堆叠中保留主导注意力分数，将整体空间复杂度大幅降低至 O((2 − ε)·L log L)，使得模型更易处理长序列输入。
• 我们提出了生成式解码器，一次性生成整个长序列输出，避免传统逐步推理过程中的误差积累，同时显著提高推理速度。

5 准备知识

我们首先给出长序列时间序列预测（LSTF）问题的定义。在固定窗口大小的滑动预测设置下，给定时间点 $t$ 的输入序列为：

$$X^t = \{x^t_1, x^t_2, \ldots, x^t_{L_x} \quad | \quad x^t_i \in \mathbb{R}^{d_x} \}$$

目标是预测对应的输出序列：

$$Y^t = \{y^t_1, y^t_2, \ldots, y^t_{L_y} \quad | \quad y^t_i \in \mathbb{R}^{d_y} \}$$

与以往研究相比，LSTF问题强调预测更长的输出序列（即 $L_y$ 更大），并且不局限于单变量预测（即允许 $d_y \geq 1$）。

5.1 编码器-解码器架构

许多流行模型采用编码器-解码器框架，将输入表示 $X^t$ 编码为隐藏状态表示 $H^t$，然后从中解码出输出序列 $Y^t$。其中：

$$H^t = \{ h^t_1, h^t_2, \ldots, h^t_{L_h} \}$$

在推理过程中，通常采用逐步生成（动态解码），即解码器根据前一状态 $h^t_k$ 和第 $k$ 步的输出，计算新隐藏状态 $h^t_{k+1}$，进而预测第 $k+1$ 个输出：$y^t_{k+1}$

5.2 输入表示

为了增强时间序列输入的全局位置上下文与局部时间结构信息，本文设计了一种统一的输入表示方法。详细内容见附录B。

6 方法

现有的时间序列预测方法大致可以分为两类：

1. 经典时间序列模型：如自回归模型、移动平均模型等，这些方法在时间序列预测中被广泛采用，具有较强的理论基础与稳定性。
2. 深度学习方法：主要基于RNN及其变体，发展出“编码-解码”预测范式，在建模非线性、长距离依赖方面具有更强的能力。

我们提出的 Informer 模型也采用了编码器-解码器架构，但专门面向长序列时间序列预测（LSTF）问题进行设计优化。整体结构请参考图2，具体细节将在下文各节详细介绍。

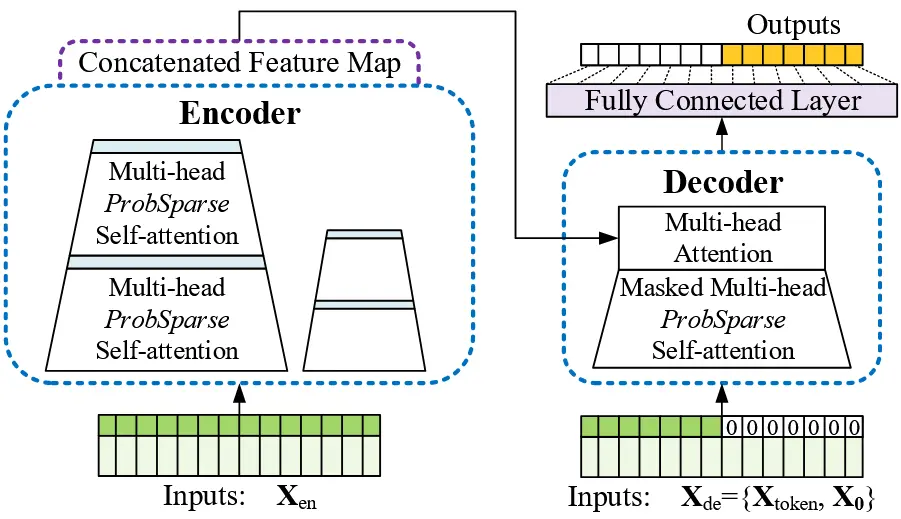
图 2：Informer 模型概览。左侧（Encoder 编码器部分）：接收超长序列输入（绿色）； 将标准的自注意力机制替换为本文提出的 ProbSparse 自注意力机制；蓝色梯形部分表示 自注意力蒸馏操作，用于提取主导注意力信息，从而大幅压缩网络规模；多个堆叠副本（stack replicas）提高模型的鲁棒性。 右侧（Decoder 解码器部分）：接收长序列输入，并将目标位置以零值填充（占位）；根据编码器输出特征图进行加权注意力组合；最终以生成式方式一次性预测出所有输出序列（橙色），无需逐步生成。

6.1 高效的自注意力机制

传统的自注意力机制由输入三元组构成：Query（Q）、Key（K） 和 Value（V），并通过缩放点积计算注意力权重：

$$A(Q, K, V) = \text{Softmax}\left(\frac{QK^\top}{\sqrt{d}}\right)V$$

其中：$Q \in \mathbb{R}^{L_Q \times d}$， $K \in \mathbb{R}^{L_K \times d}$， $V \in \mathbb{R}^{L_V \times d}$，$d$ 是输入特征维度。

为了进一步理解注意力机制，设第 $i$ 行分别为 $q_i, k_i, v_i$，则第 $i$ 个查询的注意力输出可以表示为一种概率形式的核平滑器（kernel smoother）：

$$A(q_i, K, V) = \sum_j \frac{k(q_i, k_j)}{\sum_l k(q_i, k_l)} v_j = \mathbb{E}_{p(k_j|q_i)}[v_j] \tag{1}$$

其中：

• $p(k_j|q_i) = \frac{k(q_i, k_j)}{\sum_l k(q_i, k_l)}$
• 核函数 $k(q_i, k_j) = \exp\left(\frac{q_i^\top k_j}{\sqrt{d}}\right)$，即非对称指数核。

该机制通过计算所有查询和键之间的点积来得到注意力分布，因而其时间复杂度为 $O(L_Q \cdot L_K)$，空间复杂度也为 $O(L_Q \cdot L_K)$。这是限制模型扩展到长序列输入的主要瓶颈之一。

已有研究观察到，自注意力权重的分布存在潜在的稀疏性。因此，有人提出了“选择性”的计算策略，仅保留少数有效的注意力对，以此提升效率。

• Sparse Transformer：通过分离空间位置构建稀疏图结构。
• LogSparse Transformer：引入指数步长，使每个单元关注之前的特定位置。
• Longformer：将上述方法扩展为更复杂的稀疏配置。

然而，这些方法大多基于启发式规则，对所有注意力头统一处理方式，在灵活性与进一步改进上存在限制。

为更好地设计稀疏自注意力机制，我们首先对标准注意力机制中学习到的注意力模式进行定性分析。结果发现其注意力权重呈现长尾分布：仅有少数查询-键对产生主要注意力贡献，其他则接近无效（详见附录C）。

因此，关键问题转化为：如何有效地区分这些“重要”的查询-键对？ 这也为我们后续提出的 ProbSparse Attention 奠定了基础。

6.2 查询稀疏性度量

根据公式 (1)，第 $i$ 个查询 $q_i$ 对所有键 $k_j$ 的注意力权重构成一个概率分布 $p(k_j|q_i)$，最终的注意力输出是该分布与值向量 $v_j$ 的加权组合。

在实际中，重要的点积对会导致该注意力分布远离均匀分布。如果 $p(k_j|q_i)$ 趋近于均匀分布：

$$q(k_j | q_i) = \frac{1}{L_K}$$

那么自注意力实际上就变成了对值向量 $V$ 的“平均求和”，这对原始输入几乎没有有效信息增益。

因此，我们可以利用概率分布 $p$ 与均匀分布 $q$ 之间的“相异程度”来判断一个查询是否重要。这个相异程度通过Kullback-Leibler 散度（KL散度） 来度量：

$$\text{KL}(q \| p) = \ln \sum_{l=1}^{L_K} \exp\left(\frac{q_i^\top k_l}{\sqrt{d}}\right) - \frac{1}{L_K} \sum_{j=1}^{L_K} \frac{q_i^\top k_j}{\sqrt{d}} - \ln L_K$$

去掉常数项后，我们定义第 $i$ 个查询的稀疏性度量为：

$$M(q_i, K) = \ln \left( \sum_{j=1}^{L_K} \exp\left( \frac{q_i^\top k_j}{\sqrt{d}} \right) \right) - \frac{1}{L_K} \sum_{j=1}^{L_K} \frac{q_i^\top k_j}{\sqrt{d}} \tag{2}$$

其中：第一项是 Log-Sum-Exp（LSE） 操作，表示所有点积的指数和的对数；第二项是所有点积的算术平均值。

若 $M(q_i, K)$ 值越大，说明该查询 $q_i$ 的注意力分布越稀疏、越“非均匀”，意味着它可能集中注意力于少数关键键向量，这正是长尾分布中具有主导贡献的部分。因此，这一度量可以作为一种有效筛选“重要查询”的准则，为后续构建稀疏注意力机制（如 ProbSparse Attention）提供基础。

6.3 ProbSparse 自注意力机制

基于前述的查询稀疏性度量 $M(q, K)$，我们提出了 ProbSparse 自注意力机制，其核心思想是：只保留那些注意力分布最“稀疏”的 Top-$u$ 个查询向量参与计算。公式如下：

$$A(Q, K, V) = \text{Softmax} \left( \frac{QK^\top}{\sqrt{d}} \right)V \tag{3}$$

其中：

• $Q$ 是一个稀疏矩阵，仅保留根据稀疏性度量 $M(q, K)$ 筛选出的 Top-$u$ 个查询；
• 保留下来的查询与键进行注意力计算，其余位置填 0；
• 最终计算出的注意力权重再与值 $V$ 相乘。

我们通过一个采样因子 $c$ 控制保留的查询数量：

$$u = c \cdot \ln L_Q$$

这样，ProbSparse 注意力在每个 query-key 查找中只需要计算 $O(\ln L_Q)$ 次点积操作，整层的内存复杂度降为：

$$O(L_K \cdot \ln L_Q)$$

在多头注意力机制下，每个注意力头可获得一组不同的稀疏查询-键对，这样可以有效避免信息丢失，相比统一稀疏策略更加灵活。然而，逐个计算所有查询的稀疏性度量 $M(q_i, K)$ 仍需要对每个 $q_i$ 与所有 $k_j$ 执行点积，即总计算量仍为 $O(L_Q \cdot L_K)$，并且其中的 Log-Sum-Exp 操作存在数值稳定性问题。

因此，我们进一步提出了一种经验性近似方法，用于高效地估算稀疏性度量 $M(q, K)$，从而避免遍历所有查询，提高整体计算效率。这一近似方案将在后续部分介绍。

6.4 引理 1（Lemma 1）

对于每个查询向量 $q_i \in \mathbb{R}^d$ 和键集合中的 $k_j \in \mathbb{R}^d$，我们有如下稀疏度量 $M(q_i, K)$ 的上下界：

$$\ln L_K \leq M(q_i, K) \leq \max_j \left\{ \frac{q_i^\top k_j}{\sqrt{d}} \right\} - \frac{1}{L_K} \sum_{j=1}^{L_K} \frac{q_i^\top k_j}{\sqrt{d}} + \ln L_K$$

当 $q_i \in K$ 时，该不等式同样成立。

最大值-平均值近似（Max-Mean Approximation）： 根据上述引理，我们提出了一种数值更稳定、计算更高效的近似度量方式：

$$M(q_i, K) = \max_j \left\{ \frac{q_i^\top k_j}{\sqrt{d}} \right\} - \frac{1}{L_K} \sum_{j=1}^{L_K} \frac{q_i^\top k_j}{\sqrt{d}} \tag{4}$$

该近似方法的优点包括：

• 稳定性强：最大值操作（max）对填充零值不敏感；
• 避免使用 Log-Sum-Exp：规避了数值不稳定问题；
• 计算简单：无需所有点积都保留。

稀疏采样策略： 基于长尾分布的假设，我们无需遍历所有点积对，而是仅随机采样 $U = L_K \cdot \ln L_Q$ 个 query-key 对进行计算，其余位置填充为 0。然后，在这些候选中根据上式选择 Top-$u$ 个作为有效查询。在实际应用中，我们通常令查询长度与键长度相同，即：

$$L_Q = L_K = L$$

这样，最终的 ProbSparse 自注意力机制的时间和空间复杂度可以降至：

$$O(L \cdot \ln L)$$

这为处理长序列时间序列提供了理论与实践上的高效基础。

6.5 编码器-在内存限制下支持处理更长序列输入

Informer 的编码器专为提取长序列输入中的稳健长距离依赖关系而设计。在完成统一输入表示后，第 $t$ 时刻的序列输入被表示为一个矩阵：

$$X^{t}_{\text{en}} \in \mathbb{R}^{L_x \times d_{\text{model}}}$$

为了处理长序列输入且不增加内存压力，编码器引入了一个关键机制 —— 自注意力蒸馏（Self-attention Distilling）。

由于 ProbSparse 自注意力的稀疏性，编码器输出的特征图中仍存在大量冗余的 Value 组合。因此，我们引入蒸馏操作来突出其中的主导特征，使下一层仅聚焦于更有价值的注意力信息。其基本流程如下：

$$X^{t}_{j+1} = \text{MaxPool} \left( \text{ELU} \left( \text{Conv1d}\left( [X^{t}_j]_{\text{AB}} \right) \right) \right) \tag{5}$$

其中：

• $[X^{t}_j]_{\text{AB}}$ 表示经过 Attention Block 处理后的输出；
• Attention Block 内部包含了 多头 ProbSparse 自注意力、前馈网络等核心操作；
• $\text{Conv1d}(\cdot)$：对时间维进行一维卷积（卷积核宽度为3）；
• $\text{ELU}(\cdot)$：激活函数；
• $\text{MaxPool}(\cdot)$：时间维最大池化，步长为2，用于将输入时间长度缩小一半。 该机制每堆叠一层，就对序列长度减半，从而将整体内存复杂度降低为：$O((2 - \varepsilon) \cdot L \log L)$。其中 $\varepsilon$ 是一个很小的常数。

金字塔结构与多层蒸馏堆叠
为了增强蒸馏操作的鲁棒性与信息完整性，Informer 设计了多个编码器副本（stack replicas）：

• 每个副本输入序列长度减半；
• 后续蒸馏层数也逐层递减（如图2所示构成金字塔结构）；
• 所有副本输出在维度上对齐，并拼接（concatenate） 为最终的编码器表示。

这样，Informer 能够在控制内存消耗的同时有效接收和处理超长时间序列输入，为解码器提供丰富且紧凑的上下文特征。

6.6 解码器：通过一次前向传播生成长序列输出

Informer 的解码器结构采用了标准的 Transformer 解码器架构（如图 2 所示），由两个完全相同的多头注意力层（Multi-head Attention Layers） 堆叠而成。但与传统方法不同，Informer 引入了生成式推理（Generative Inference） 来缓解长序列预测时的推理速度下降问题。

解码输入结构
我们构造解码器的输入为：

$$X^t_{\text{de}} = \text{Concat}(X^t_{\text{token}}, X^t_0) \in \mathbb{R}^{(L_{\text{token}} + L_y) \times d_{\text{model}}} \tag{6}$$

其中：

• $X^t_{\text{token}} \in \mathbb{R}^{L_{\text{token}} \times d_{\text{model}}}$：起始 token（start token）；
• $X^t_0 \in \mathbb{R}^{L_y \times d_{\text{model}}}$：目标序列的占位符，初始值为 0。 在 ProbSparse 自注意力计算中应用了 masked attention，通过将未来位置的点积设为 $-\infty$，阻止当前位置访问未来信息，避免了自回归。

最终输出通过一个全连接层（Fully Connected Layer）映射为预测值，其输出维度 $d_y$ 取决于是单变量预测还是多变量预测。

生成式推理（Generative Inference）
在自然语言处理中的动态解码中，start token 通常是一个特殊标志；而在Informer中，我们采用生成式处理方式：从输入序列中截取一段真实数据（例如预测序列前的一段），作为 start token。举例说明：

• 若要预测 168 个时间点（7 天温度），可取预测目标前的已知 5 天作为 start token：

$$X_{\text{de}} = \{ X_{5d}, X_0 \}$$

其中 $X_0$ 中包含预测序列对应时间戳（例如目标周的时间信息）。

• 然后，Informer 解码器仅通过一次前向传播即可预测整个长序列输出，无需传统逐步预测，避免了动态解码中常见的误差累积与推理效率低下问题。

损失函数

我们使用 均方误差（MSE）损失函数 来衡量预测输出与目标序列之间的误差：

$$\mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2$$

该损失从解码器输出端反向传播，贯穿整个模型参数进行更新。这种非自回归、一次性推理的生成式解码方式，不仅提高了预测效率，还增强了长序列预测的稳定性，是 Informer 区别于传统 Transformer 的重要创新之一。

7 超参数设置与实验配置

7.1 超参数调优

• 使用**网格搜索（Grid Search）**方式对超参数进行调优；
• 超参数搜索的详细范围详见附录 E.3；
• Informer 编码器结构：
  • 包含一个 3 层主堆叠（full input）；
  • 一个 1 层副堆叠（输入长度为主堆叠的 1/4）；
• 解码器为 2 层结构；
• 优化器采用 Adam，初始学习率为 $1 \times 10^{-4}$，每轮训练后衰减为原来的一半；
• 总训练轮数为 8 轮，并设置了Early Stopping；
• 批大小（Batch Size）为 32；
• 所有数据集输入均进行了 零均值标准化（zero-mean normalization）。

7.2 LSTF预测设置

• 在长序列预测场景下，逐步扩展预测窗口 $L_y$ 的长度：
  • 对于 ETTh、ECL、Weather 数据集：预测窗口为 {1d, 2d, 7d, 14d, 30d, 40d}；
  • 对于 ETTm 数据集：预测窗口为 {6h, 12h, 24h, 72h, 168h}。

7.3 评估指标

使用以下两种指标评估预测性能（多变量预测时取平均）：

• 均方误差（MSE）：

$$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$$

• 平均绝对误差（MAE）：

$$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$

评估采用滑动窗口方式，滑动步长为 1。

7.4 实验平台

• 所有模型均在 单张 Nvidia V100 GPU（32GB 显存） 上进行训练与测试；
• 源代码开源，地址如下： https://github.com/zhouhaoyi/Informer2020 (opens new window)

8 附录B：统一输入表示

在传统的时间序列建模中：

• RNN 模型（如 LSTM、GRU 等）依赖其循环结构自身捕捉时间信息，对时间戳信息依赖较弱；
• 标准 Transformer 使用点对点的自注意力机制，通常仅利用时间戳作为局部位置编码（positional encoding）。

然而，在 长序列时间序列预测（LSTF） 问题中，模型需要捕捉更远距离的依赖关系，光靠局部时间顺序是不够的。这就要求输入表示具备：

• 全局时间上下文（如周、月、年等层级信息）；
• 通用时间信息（如节假日、事件等不可预测但结构性的重要时点）。

标准 Transformer 的自注意力机制难以自然利用这些信息，容易导致编码器和解码器的 Query-Key 失配，从而影响预测性能。

为此，作者提出了统一输入表示方法，如下图 6 所示，并包含以下三个部分：

8.1 保留局部时间信息：位置编码（Positional Encoding）

使用标准的正余弦位置编码：

$$\text{PE}(\text{pos}, 2j) = \sin\left(\frac{\text{pos}}{(2L_x)^{2j/d_{\text{model}}}}\right), \quad \text{PE}(\text{pos}, 2j+1) = \cos\left(\frac{\text{pos}}{(2L_x)^{2j/d_{\text{model}}}}\right) \tag{7}$$

其中 $j \in \{1, \dots, \lfloor d_{\text{model}}/2 \rfloor \}$，用于表示时间点在序列中的相对位置。

8.2 引入全局时间戳：时间嵌入（Time Stamp Embedding）

• 对每一种全局时间戳（如“星期几”、“月份”、“节假日”）设置一个可学习的嵌入向量 $\text{SE(pos)}$；
• 时间戳的词表大小限制在约 60（如按分钟粒度），以保证在长序列输入下计算可控；
• 多种时间戳嵌入后将逐一相加进入表示。

8.3 标量上下文表示投影（Scalar Projection）

将原始输入标量 $x^t_i$ 使用 一维卷积投影到模型维度空间中：

$$u^t_i = \text{Conv1D}(x^t_i), \quad \text{卷积核宽度} = 3, \text{stride} = 1$$

最终输入表示拼接方式如下：

$$X^t_{\text{feed}}[i] = \alpha u^t_i + \text{PE}(L_x \cdot (t-1) + i) + \sum_p \text{SE}_p(L_x \cdot (t-1) + i) \tag{8}$$

其中：

• $i \in \{1, \dots, L_x\}$；
• $\alpha$ 为标量投影与时间戳嵌入之间的权重系数，若输入已标准化，则推荐设置为 1。

8.4 总结：

这种统一输入表示方法融合了：

• 原始输入内容（标量）；
• 局部位置信息；
• 多层次的全局时间上下文。 从而为自注意力机制提供了结构化的时间线索，极大提升了在 LSTF 场景下的表现能力。

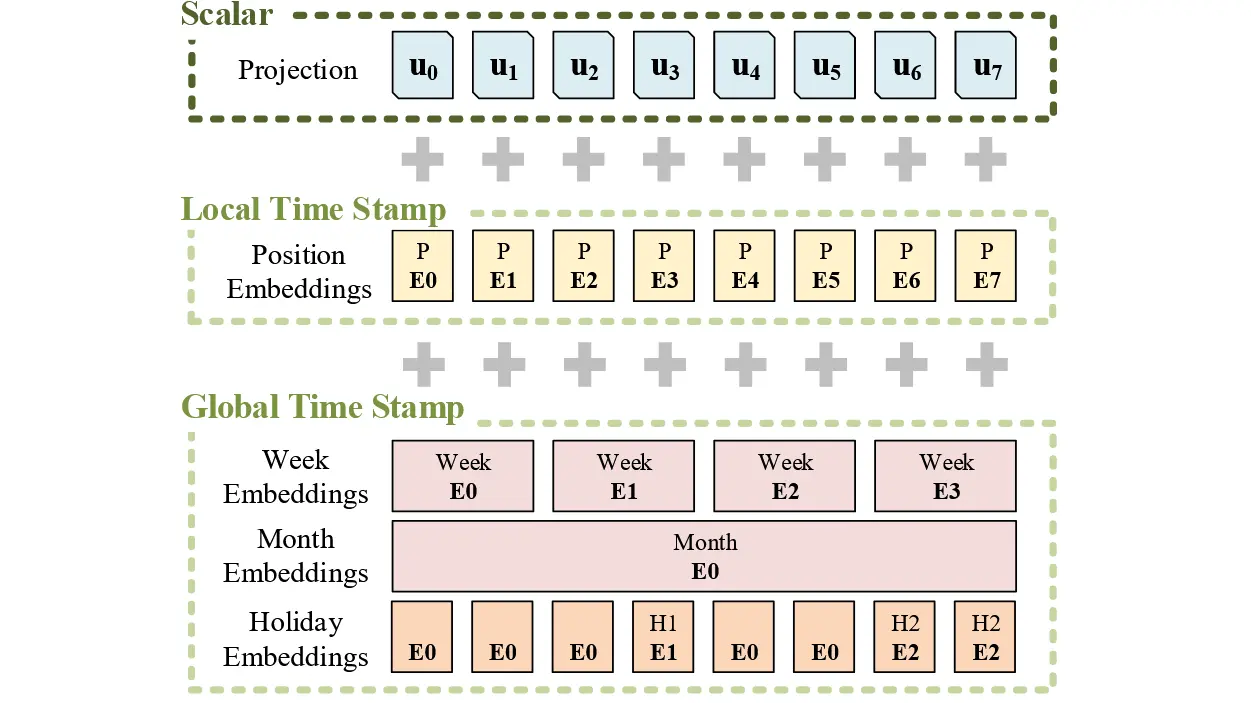图 6：Informer 的输入表示结构。Informer 的输入嵌入由以下三个部分组成：1. 标量投影（Scalar Projection）：将原始输入的数值特征（如温度、电量等）通过一维卷积映射到模型的向量空间。2. 局部时间戳（位置编码，Position）：使用固定的正余弦位置编码，捕捉输入序列中每个时间点的相对位置信息。3. 全局时间戳嵌入（Global Time Stamp Embeddings）： 包括分钟、小时、星期、月份、节假日等多层次时间信息，每种时间字段都有独立的可学习嵌入向量。这三部分相加后共同组成了 Informer 模型的统一输入表示，使其具备对时间结构的全面感知能力。