1 Time Series Transformer（TST）

介绍一篇关于时序预测相关一篇论文：A Transformer-based Framework for Multivariate Time Series Representation Learning。具体来说它是一个做时间序列分类（回归） 的模型。
论文地址：https://arxiv.org/abs/2010.02803 (opens new window)
GitHub：https://github.com/gzerveas/mvts_transformer (opens new window)

2 一句话总结这篇论文

就是将 Transformer 用到了时序分类/回归，它先使用类似“完形填空”的方式预训练，然后在特定下游任务（分类/回归）微调。代码简单易懂。

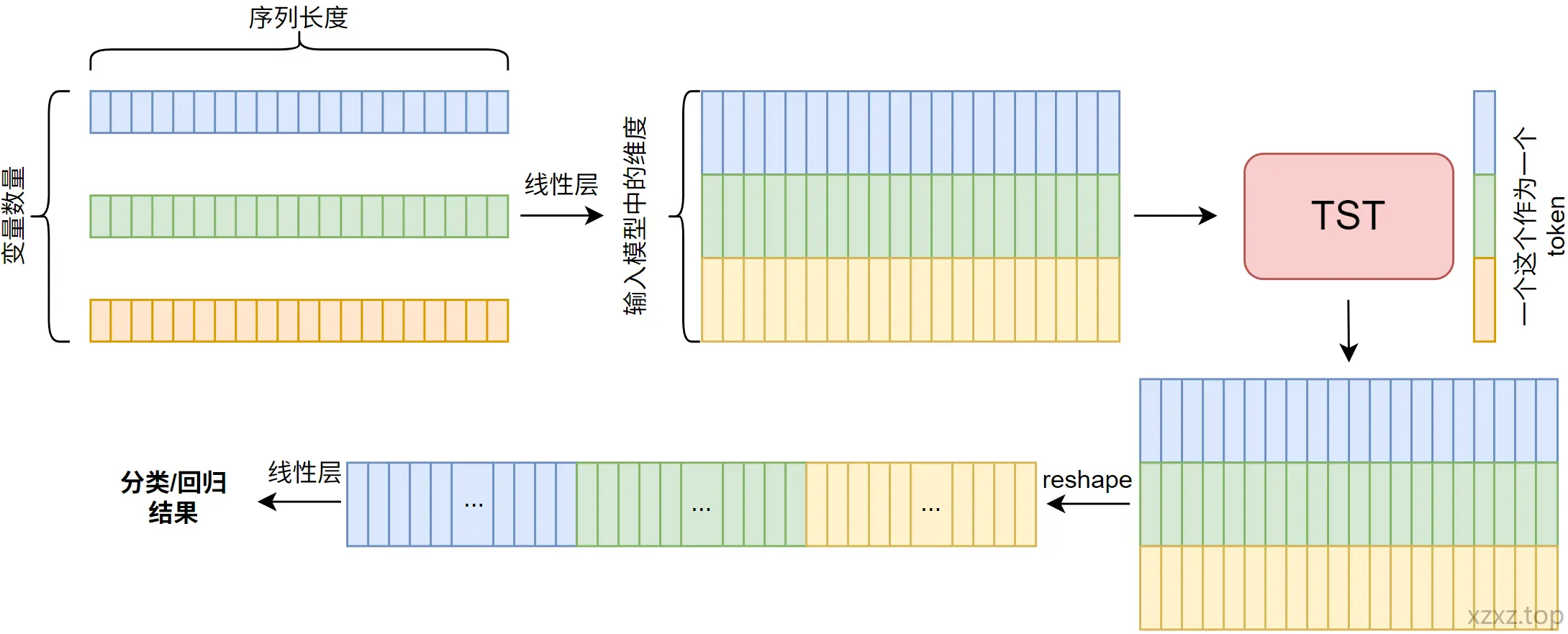
上图为我根据它的代码画的更详细的数据流向图。

3 摘要

本文提出了一个基于 Transformer 编码器架构的多变量时间序列表征学习的新型框架。该框架包含一个无监督预训练机制，在下游任务中，即使不借助额外的未标注数据，仅通过重复利用已有数据样本，也能显著优于完全依赖监督学习的表现。 其在多个具有不同特征、来自不同行业领域的公开多变量时间序列数据集上对该框架进行了评估，结果表明：无论在回归还是分类任务中，该方法均显著优于当前最先进的其他方法，甚至在训练样本仅有几百条的情况下依然表现出色。 鉴于在科学界与工业界对无监督学习的广泛关注，这一成果具有重要意义——它是首个被证明能在多变量时间序列回归和分类任务中突破现有技术性能上限的无监督方法。

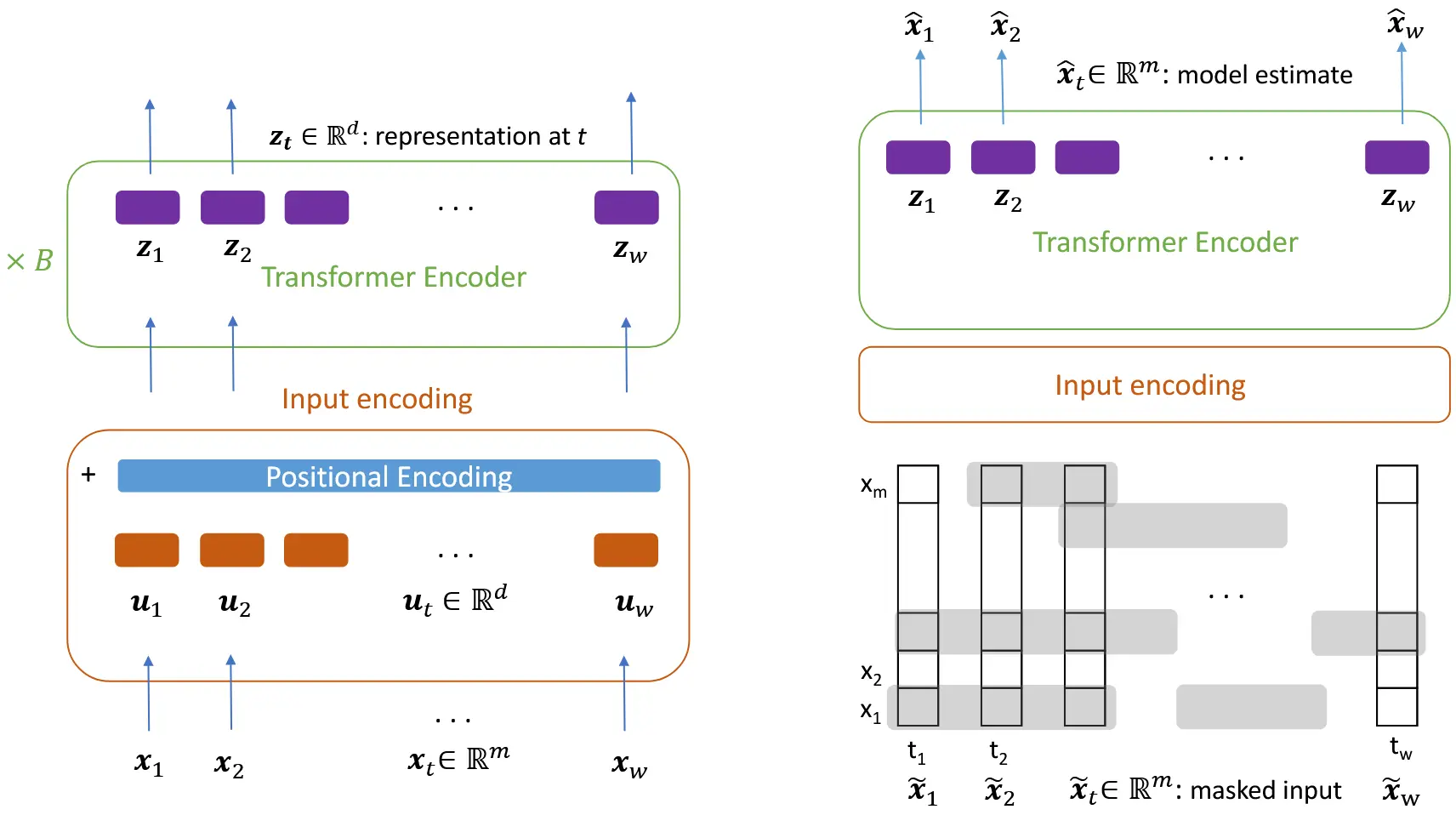
图 1：左图展示了适用于所有任务的通用模型架构。在每个时间步 $t$，特征向量 $x_t$ 通过线性投影映射为一个维度为 $d$ 的向量 $u_t$，该维度与模型内部表示向量的维度相同。然后将位置编码添加到 $u_t$ 上，作为输入送入第一层自注意力模块，用于生成 keys、queries 和 values。右图展示了无监督预训练任务的训练设置。我们对输入中每个变量序列独立地掩盖一部分比例 $r$，在每个变量上，掩码将作用于平均长度为 $l_m$ 的时间片段，每个被掩盖的片段后跟随一个未被掩盖的片段，其平均长度为 $l_u = \frac{1 - r}{r} l_m$。在最终表示向量 $z_t$ 上接一个线性层，在每个时间步，模型尝试预测完整、未被扰动的输入向量 $x_t$；但在计算均方误差（MSE）损失时，只考虑那些被掩盖位置的预测值。

4 方法

4.1 Base model

每个训练样本 $X \in \mathbb{R}^{w \times m}$ 是一个长度为 $w$、包含 $m$ 个变量的多变量时间序列，可以表示为由 $w$ 个特征向量 $x_t \in \mathbb{R}^m$ 构成的序列：

$$X = [x_1, x_2, \ldots, x_w] \in \mathbb{R}^{w \times m}$$

原始的特征向量 $x_t$ 首先会被标准化（对每个维度，在整个训练集上减去均值并除以方差），然后被线性投影到一个 $d$ 维向量空间中，其中 $d$ 是 Transformer 模型中序列元素表示的维度（通常被称为“模型维度”）：

$$u_t = W_p x_t + b_p \tag{1}$$

其中，$W_p \in \mathbb{R}^{d \times m}$、$b_p \in \mathbb{R}^d$ 是可学习参数，$u_t \in \mathbb{R}^d$，$t = 0, \ldots, w$ 是模型的输入向量。这些向量在加入位置编码后，将用于构建自注意力层中的 query、key 和 value。 我们还指出，上述公式同样适用于单变量时间序列（即 $m = 1$），尽管本研究中仅在多变量时间序列上进行了评估。我们还注意到，输入向量 $u_t$ 不一定非得来自某个时间步 $t$ 的（变换后的）特征向量。由于模型的计算复杂度随着输入序列长度 $w$ 增长为 $\mathcal{O}(w^2)$，而部分参数的数量增长为 $\mathcal{O}(w)$，因此当数据的时间粒度（时间分辨率）非常高时，为了获得 $u_t$，可以采用一个一维卷积层，该卷积层有1个输入通道、$d$ 个输出通道，每个卷积核 $K_i$ 的大小为 $(k, m)$，其中 $k$ 是时间步数量上的宽度，$i$ 是输出通道编号：

$$u_t^i = u(t, i) = \sum_j \sum_h x(t + j, h) K_i(j, h), \quad i = 1, \dots, d \tag{2}$$

通过这种方式，可以通过使用大于1的步幅（stride）或膨胀率（dilation）来控制时间分辨率。此外，尽管在本工作中我们仅使用了公式（1），也可以使用公式（2）来计算自注意力层的键（keys）和查询（queries），而使用公式（1）来计算值（values）。这在处理单变量时间序列时尤其有用，因为如 Li 等人所指出的那样，在这种情况下自注意力机制可能会匹配所有具有相似自变量值的时间步。尽管我们观察到在某些由较长且维度较低的时间序列组成的数据集上使用一维卷积层可以提升性能，但出于提出统一架构框架的考虑，在本文中我们未采用这些结果。 最后，由于 Transformer 是一种前馈结构，对输入的顺序不敏感，因此为了让模型感知时间序列的顺序性，我们向输入向量 $U \in \mathbb{R}^{w \times d} = [u_1, \ldots, u_w]$ 中加入了位置编码 $W_{\text{pos}} \in \mathbb{R}^{w \times d}$，使得最终的输入为：

$$U' = U + W_{\text{pos}}$$

我们没有采用 [32] 最初提出的确定性正弦位置编码，而是使用了完全可学习的位置编码，因为我们观察到在本文涉及的所有数据集上，它们的表现都更好。 根据模型的表现，我们还发现这些位置编码通常不会显著干扰时间序列中的数值信息，这一点与词嵌入中的情况类似；我们推测原因是这些位置编码在训练过程中学会了分布在一个与时间序列投影后表示所处空间近似正交的子空间中。而在高维空间中，满足这种近似正交的条件要容易得多。 在处理时间序列数据时，一个重要的考虑因素是：不同的样本在序列长度上可能存在较大的差异。在我们的框架中，这一问题得到了有效解决：我们首先为整个数据集设定一个最大的序列长度 $w$，对于那些较短的样本，我们用任意值进行填充（padding）。随后，我们生成一个填充掩码（padding mask），在计算自注意力分布的 softmax 之前，将一个很大的负数加到填充值对应的位置的注意力得分上。这样可以强制模型完全忽略这些填充位置，同时仍然可以对多个样本进行高效的并行批量处理。 在自然语言处理（NLP）中，Transformer 通常在每个编码器模块中的自注意力和前馈网络之后使用层归一化（Layer Normalization），这一做法相比批归一化（Batch Normalization）带来了显著的性能提升，这也是 [32] 最初的建议。 然而在本工作中，我们改为使用批归一化，因为它可以减轻时间序列中**异常值（outlier）**带来的影响——这是 NLP 的词嵌入中不常出现的问题。 此外，批归一化在 NLP 中效果较差，主要是由于样本长度的极端变化（如句子长度差异很大）[28]；而在我们所研究的数据集中，这种长度变化相对较小。 在表 1 中，我们展示了：批归一化在某些数据集上确实可以比层归一化带来显著的性能提升，尽管其效果的大小会根据数据集的具体特性有所不同。

4.2 回归与分类

再前面介绍的基础模型架构（见图 1）可以通过以下修改，用于回归和分类任务： 将所有时间步对应的最终表示向量 $z_t \in \mathbb{R}^d$ 拼接成一个单一向量：

$$\bar{z} \in \mathbb{R}^{d \cdot w} = [z_1; z_2; \ldots; z_w]$$

该拼接向量作为输入送入一个线性输出层，其参数为：

• $W_o \in \mathbb{R}^{n \times (d \cdot w)}$：权重矩阵
• $b_o \in \mathbb{R}^n$：偏置向量 其中 $n$ 是需要预测的标量数量（对于回归任务，通常 $n = 1$），或者是分类任务中的类别数。 模型输出的预测值为：

$$\hat{y} = W_o \bar{z} + b_o \tag{3}$$

在回归任务中，单个数据样本的损失函数就是简单的平方误差：

$$L = \| \hat{y} - y \|^2$$

其中 $y \in \mathbb{R}^n$ 是对应的真实标签值。 我们在此明确指出：本工作的“回归”是指对整个时间序列样本预测一个全局的数值。这个全局数值与时间序列中每个时间步的变量是不同性质的。 例如：假设给定一个时间序列，其中包含一个房屋中9个房间在一天中同时记录的温度和湿度，以及相关的天气和气候数据（例如温度、气压、湿度、风速、能见度和露点温度）等变量。那么我们希望预测的全局数值是这个房屋在这一天内的总能耗（以 kWh 为单位）。 参数 $n$ 表示要预测的全局标量数量（或者是要估计的目标向量的维度）。 在分类任务中，模型的预测值 $\hat{y}$ 会进一步通过一个 softmax 函数，从而得到一个对所有类别的概率分布。然后，使用该分布与真实的类别标签之间的 交叉熵（cross-entropy） 作为该样本的损失函数。 最后，在对预训练模型进行微调时，我们允许所有参数都参与训练；相反，如果只训练输出层、而将其余所有层“冻结”（不更新），那等价于仅使用一组静态的、预提取的时间序列表示。 在表 2 中，我们展示了完全可训练模型与使用静态表示之间在训练速度与性能表现方面的权衡。

4.3 无监督（自监督）预训练

作为我们模型的无监督预训练任务，我们采用了一种自回归的输入去噪任务：具体而言，我们将输入的一部分设置为 0，并让模型去预测这些被遮盖（mask）掉的数值。相应的训练设置如图 1 的右侧所示。 我们为每个训练样本和每一轮训练独立地生成一个二值噪声掩码 $M \in \mathbb{R}^{w \times m}$，然后通过逐元素乘法将掩码应用到输入上：

$$\tilde{X} = M \odot X$$

在每个变量（每列的长度为 $w$）中，平均有一部分比例 $r$ 被置为 0。我们通过交替生成 0 段和 1 段来实现这一点。 我们选择使用马尔可夫状态转移方式来控制掩码的结构，使得每一段被遮盖的连续 0 序列，其长度服从平均值为 $l_m$ 的几何分布。每段遮盖之后跟随一个未遮盖（值为 1）的序列，其平均长度为：

$$l_u = \frac{1 - r}{r} \cdot l_m$$

在所有实验中，我们设置 $l_m = 3$。 我们之所以不简单地使用伯努利分布（即以概率 $r$ 随机遮盖每个元素），是因为这样可能会产生很多很短的遮盖片段（例如只遮一个值），这些短片段往往可以通过复制相邻数值或取其平均值轻松预测出来，导致模型学不到有意义的模式。为了使模型遇到较长的遮盖序列并从中学习，就需要足够高的遮盖比例 $r$，但这样又会导致任务变得过于困难。 按照上述方法，在每个时间步，平均会有 $r \cdot m$ 个变量被遮盖。 我们通过实验发现：当 $r = 0.15$ 时效果良好，并在所有实验中采用了这一设置。 需要注意的是：这种输入遮盖方式不同于 NLP 模型（如 BERT）中的“完形填空式（cloze-type）遮盖”，后者通常使用一个特殊的掩码 token 替换整个词向量（即完全替换某一时间步的全部特征向量）。 而我们选择的遮盖模式有助于模型：

• 同时关注每个变量自身中被遮位置的前后上下文；
• 也关注其他变量在同一时间步上的值； 这样能够促使模型学习多变量之间的依赖关系。 我们在表 3 中展示了：这种遮盖方式在输入去噪任务中比其他方法更有效。 在最终表示向量 $z_t \in \mathbb{R}^d$ 的基础上，使用一个线性层，其参数为 $W_o \in \mathbb{R}^{m \times d}$、$b_o \in \mathbb{R}^m$，模型在每个时间步 $t$ 上并行地输出对完整、未被扰动的输入向量 $x_t$ 的预测值 $\hat{x}_t$：

$$\hat{x}_t = W_o z_t + b_o \tag{4}$$

然而，在计算每个样本的均方误差（MSE）损失时，只考虑那些被遮盖位置的预测值，即掩码集合：

$$M \equiv \{(t, i) \mid m_{t,i} = 0\}$$

其中 $m_{t,i}$ 是掩码矩阵 $M$ 中的位置元素。 于是，损失函数定义为：

$$L_{\text{MSE}} = \frac{1}{|M|} \sum_{(t, i) \in M} \left( \hat{x}(t, i) - x(t, i) \right)^2 \tag{5}$$

这一目标函数与去噪自编码器（denoising autoencoder）常用的方法不同，后者通常在高斯噪声扰动下对整个输入进行重建，并将全部输入纳入损失。 此外，这种遮盖方式也不同于常见的输入嵌入上的 Dropout，两者在“被遮值的统计分布”以及“是否决定损失项的计算”上都有本质区别。实际上，在训练我们所有的有监督与无监督模型时，我们还额外使用了 10% 的 Dropout。

5 代码

网络结构还是比较简单的，预训练模型网络结构与回归和分割模型网络结构就最后的输出层不一样。

5.1 预训练模型网络结构

class TSTransformerEncoder(nn.Module):

    def __init__(self, feat_dim, max_len, d_model, n_heads, num_layers, dim_feedforward, dropout=0.1,
                 pos_encoding='fixed', activation='gelu', norm='BatchNorm', freeze=False):
        super(TSTransformerEncoder, self).__init__()

        self.max_len = max_len
        self.d_model = d_model
        self.n_heads = n_heads

        self.project_inp = nn.Linear(feat_dim, d_model)
        self.pos_enc = get_pos_encoder(pos_encoding)(d_model, dropout=dropout*(1.0 - freeze), max_len=max_len)

        if norm == 'LayerNorm':
            encoder_layer = TransformerEncoderLayer(d_model, self.n_heads, dim_feedforward, dropout*(1.0 - freeze), activation=activation)
        else:
            encoder_layer = TransformerBatchNormEncoderLayer(d_model, self.n_heads, dim_feedforward, dropout*(1.0 - freeze), activation=activation)

        self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers)
        self.output_layer = nn.Linear(d_model, feat_dim)
        self.act = _get_activation_fn(activation)
        self.dropout1 = nn.Dropout(dropout)
        self.feat_dim = feat_dim

    def forward(self, X, padding_masks):
        """
        Args:
            X: (batch_size, seq_length, feat_dim) torch tensor of masked features (input)
            padding_masks: (batch_size, seq_length) boolean tensor, 1 means keep vector at this position, 0 means padding
        Returns:
            output: (batch_size, seq_length, feat_dim)
        """

        # permute because pytorch convention for transformers is [seq_length, batch_size, feat_dim]. padding_masks [batch_size, feat_dim]
        inp = X.permute(1, 0, 2)
        inp = self.project_inp(inp) * math.sqrt(
            self.d_model)  # [seq_length, batch_size, d_model] project input vectors to d_model dimensional space
        inp = self.pos_enc(inp)  # add positional encoding
        # NOTE: logic for padding masks is reversed to comply with definition in MultiHeadAttention, TransformerEncoderLayer
        output = self.transformer_encoder(inp, src_key_padding_mask=~padding_masks)  # (seq_length, batch_size, d_model)
        output = self.act(output)  # the output transformer encoder/decoder embeddings don't include non-linearity
        output = output.permute(1, 0, 2)  # (batch_size, seq_length, d_model)
        output = self.dropout1(output)
        # Most probably defining a Linear(d_model,feat_dim) vectorizes the operation over (seq_length, batch_size).
        output = self.output_layer(output)  # (batch_size, seq_length, feat_dim)

        return output

5.2 回归和分割模型网络结构

class TSTransformerEncoderClassiregressor(nn.Module):
    """
    Simplest classifier/regressor. Can be either regressor or classifier because the output does not include
    softmax. Concatenates final layer embeddings and uses 0s to ignore padding embeddings in final output layer.
    """

    def __init__(self, feat_dim, max_len, d_model, n_heads, num_layers, dim_feedforward, num_classes,
                 dropout=0.1, pos_encoding='fixed', activation='gelu', norm='BatchNorm', freeze=False):
        super(TSTransformerEncoderClassiregressor, self).__init__()

        self.max_len = max_len
        self.d_model = d_model
        self.n_heads = n_heads

        self.project_inp = nn.Linear(feat_dim, d_model)
        self.pos_enc = get_pos_encoder(pos_encoding)(d_model, dropout=dropout*(1.0 - freeze), max_len=max_len)

        if norm == 'LayerNorm':
            encoder_layer = TransformerEncoderLayer(d_model, self.n_heads, dim_feedforward, dropout*(1.0 - freeze), activation=activation)
        else:
            encoder_layer = TransformerBatchNormEncoderLayer(d_model, self.n_heads, dim_feedforward, dropout*(1.0 - freeze), activation=activation)

        self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers)
        self.act = _get_activation_fn(activation)
        self.dropout1 = nn.Dropout(dropout)
        self.feat_dim = feat_dim
        self.num_classes = num_classes
        self.output_layer = self.build_output_module(d_model, max_len, num_classes)

    def build_output_module(self, d_model, max_len, num_classes):
        output_layer = nn.Linear(d_model * max_len, num_classes)
        return output_layer

    def forward(self, X, padding_masks):
        """
        Args:
            X: (batch_size, seq_length, feat_dim) torch tensor of masked features (input)
            padding_masks: (batch_size, seq_length) boolean tensor, 1 means keep vector at this position, 0 means padding
        Returns:
            output: (batch_size, num_classes)
        """
        # X: (batch_size, seq_length, feat_dim) torch.Size([64, 144, 9]), padding_masks: (batch_size, seq_length) torch.Size([64, 144])
        # permute because pytorch convention for transformers is [seq_length, batch_size, feat_dim]. padding_masks [batch_size, feat_dim]
        inp = X.permute(1, 0, 2)    # torch.Size([144, 64, 9])
        inp = self.project_inp(inp) * math.sqrt(
            self.d_model)  # torch.Size([144, 64, 64]) [seq_length, batch_size, d_model] project input vectors to d_model dimensional space
        inp = self.pos_enc(inp)  # torch.Size([144, 64, 64]) add positional encoding
        # NOTE: logic for padding masks is reversed to comply with definition in MultiHeadAttention, TransformerEncoderLayer
        output = self.transformer_encoder(inp, src_key_padding_mask=~padding_masks)  # torch.Size([144, 64, 64]) (seq_length, batch_size, d_model)
        output = self.act(output)  # torch.Size([144, 64, 64]) the output transformer encoder/decoder embeddings don't include non-linearity
        output = output.permute(1, 0, 2)  # torch.Size([64, 144, 64]) (batch_size, seq_length, d_model)
        output = self.dropout1(output)  # torch.Size([64, 144, 64])

        # Output
        output = output * padding_masks.unsqueeze(-1)  # torch.Size([64, 144, 64]) zero-out padding embeddings
        output = output.reshape(output.shape[0], -1)  # torch.Size([64, 9216]) (batch_size, seq_length * d_model)
        output = self.output_layer(output)  # (batch_size, num_classes) torch.Size([64, 25])

        return output