Protein function prediction as approximate semantic entailment

Journal: Nature Machine Intelligence (IF 23.9) Published: 2024年2月14日 开源地址：https://github.com/bio-ontology-research-group/deepgo2

GO: Gene Ontology

基因本体论（Gene Ontology，简称GO）是一个大型的国际合作生物信息学项目。它的核心目标是创建一个标准化的、动态更新的、可被计算机理解的词汇体系，用来全面地描述基因和蛋白质在各个生物体中所扮演的角色。 简单来说，GO提供了一套“标准语言”，让全世界的科学家能够用统一、精确的方式来描述基因和蛋白质的功能，从而方便数据的交换、比较和分析。

- biological_process (GO:0008150)  [生物学过程]
  - cellular process (GO:0009987)  [细胞过程]
    - cell death (GO:0008219)  [细胞死亡]
      - programmed cell death (GO:0012501)  [程序性细胞死亡]
        - is_a -> apoptotic process (GO:0006915)  [细胞凋亡过程]

这个结构清晰地显示了“细胞凋亡过程”是一个非常具体的概念，它从属于“程序性细胞死亡”，而“程序性细胞死亡”又从属于更宽泛的“细胞死亡”等概念。

Gene Ontology的核心组成部分

GO通过三个独立的、但又相互关联的本体（Ontology）或领域（Domain）来描述基因产物（即蛋白质或RNA）的生物学知识。 这三个领域分别是：

1. 分子功能 (Molecular Function, MFO)：

   • 定义：描述基因产物在分子层面上的“工作”或“活动”。 这指的是基因产物本身具备的能力，例如与什么分子结合，或者催化什么化学反应。
   • 特点：这个领域的描述不涉及具体的时间、地点或与其他分子的协作。它只关注该分子“能做什么”。
   • 例子：“催化活性” (catalytic activity)、“DNA结合” (DNA binding) 或“转运蛋白活性” (transporter activity)。

2. 生物学过程 (Biological Process, BPO)：

   • 定义：描述由一个或多个分子功能有序组合而成的、更大范围的生物学事件或目标。 它回答的是基因产物参与了“哪个生物学故事”。
   • 特点：一个生物学过程通常需要多个基因产物的协同作用才能完成。
   • 例子：“DNA修复” (DNA repair)、“细胞信号传导” (signal transduction) 或“新陈代谢” (metabolic process)。一个参与“DNA修复”的蛋白质，其“分子功能”可能是“DNA结合”和“核酸内切酶活性”。

3. 细胞组分 (Cellular Component, CCO)：

   • 定义：描述基因产物在细胞中所处的位置，或者说它是哪个细胞结构的组成部分。 它回答的是基因产物“在哪里工作”。
   • 特点：这包括了从大的细胞器到微小的蛋白质复合物。
   • 例子：“细胞核” (nucleus)、“线粒体” (mitochondrion)、“细胞质” (cytoplasm) 或“核糖体” (ribosome)。

Gene Ontology的结构特点

GO不仅仅是一个简单的词汇列表，它具有严谨的逻辑结构：

• 层级结构：GO的词条（GO term）之间存在明确的父子关系，形成一个有向无环图（Directed Acyclic Graph, DAG）的结构。 这意味着一个具体的词条（子词条）可以从属于一个或多个更宽泛的词条（父词条）。例如，“线粒体内膜”是“线粒体膜”的子集，也是“内膜系统”的子集。
• “真路径规则” (True Path Rule)：如果一个基因产物被注释到了某个GO词条，那么它也必然属于该词条的所有上级（父）词条。这使得研究人员可以根据需要，在不同详细程度上进行功能分析。

Gene Ontology的应用

GO在现代生物学和生物信息学研究中扮演着至关重要的角色，其主要应用包括：

• 功能注释 (Functional Annotation)：科学家们通过实验数据，将基因和蛋白质与最能描述其功能的GO词条关联起来。这个过程称为“功能注释”。
• 功能富集分析 (Functional Enrichment Analysis)：这是GO最常见的应用之一。例如，当研究人员通过高通量实验（如基因芯片或转录组测序）得到一个包含上百个差异表达基因的列表时，他们可以使用GO来分析这些基因主要集中在哪些生物学过程或分子功能上，从而揭示实验处理可能导致的生物学变化。
• 模型生物数据整合：由于GO的标准化特性，它可以用来比较不同物种（如人类、小鼠、酵母）的基因功能，促进了知识的迁移和整合。
• 构建知识库：GO是构建大型生物学知识库（如UniProtKB/Swiss-Prot）的基石，为自动化功能预测和系统生物学研究提供了支持。

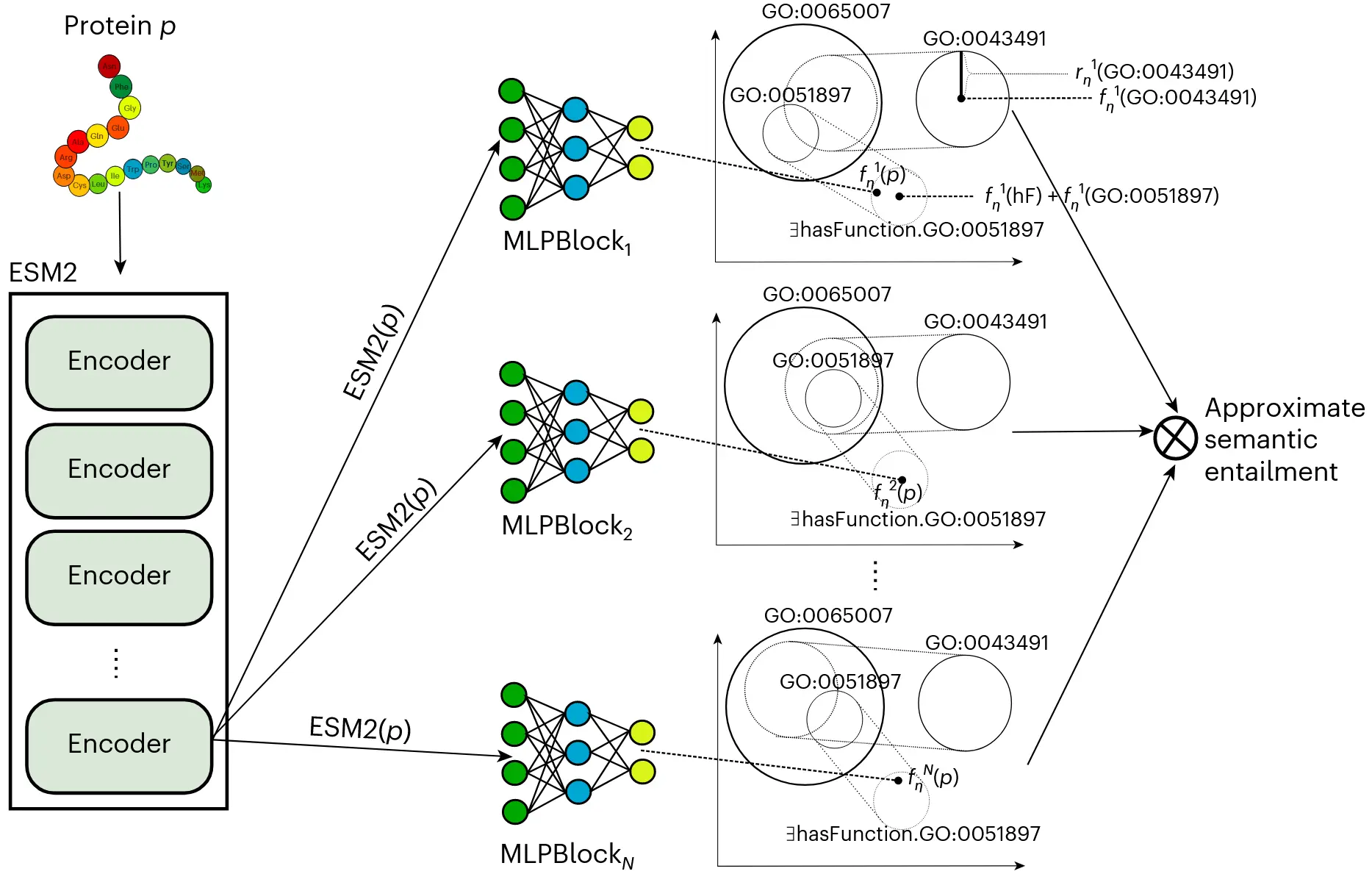
模型结构

结构：

DeepGO-SE是一个端到端的神经-符号混合模型。其核心机制可以分解为以下几个部分：

1. 蛋白质序列的向量化表示

模型采用 ESM2 (Evolutionary Scale Modeling 2)，一个基于Transformer架构的大型语言模型。

• 输入：蛋白质的氨基酸序列。
• 输出：一个能够捕捉蛋白质深层生物化学、结构和进化信息的特征向量 ESM2(p)。

2. GO知识库的几何化表示：ELEmbeddings

为了让神经网络能够“理解”GO的逻辑公理，论文采用了ELEmbeddings技术。

• 原理：该技术将描述逻辑本体（如GO）嵌入到一个欧几里得空间中。
• 实现：
  • 每个GO术语（class）C被表示为一个n维球体（n-ball），由其中心向量 c 和半径 r(c) 定义。
  • GO的公理被翻译成几何约束。例如，公理 C ⊑ D (C是D的子类) 被建模为要求C的n维球体必须完全包含在D的n维球体之内。
  • 这些几何约束被转化为一个可微的损失函数（loss function），可以在模型训练过程中进行优化，从而迫使模型学习到一个在几何上满足GO逻辑的表示空间。

3. 核心机制：近似语义蕴含

这是论文最具创新性的部分，直接对应其标题。

• 语义蕴含 (Semantic Entailment) 的定义：在逻辑学中，一个理论 T（此处指GO的所有公理）语义上蕴含一个陈述 φ（此处指“蛋白质p具有功能c”），记为 T ⊨ φ，当且仅当在所有使 T 为真的模型（即解释，interpretation）中，φ 也为真。
• 计算上的挑战：一个理论的模型集合 Mod(T) 通常是无限的，因此直接计算语义蕴含是不可行的。
• DeepGO-SE的近似方案：
  1. 学习有限模型集合：模型不尝试遍历无限的模型空间，而是通过 N 个并行的多层感知机（MLP）模块（MLPBlock）学习生成 N 个不同的、但都近似满足GO公理的有限模型/世界 {ℐ₁, ℐ₂, ..., ℐₙ}。
  2. 在每个模型中进行预测：对于一个蛋白质 p，其ESM2嵌入被分别输入到这 N 个MLP中，投影到 N 个不同的几何表示空间。在每个空间 ℐᵢ 中，模型计算陈述 hasFunction(p, c) 的真值（truth value）。在几何上，这对应于蛋白质 p 的投影向量 fᵢ(p) 落入GO术语 c 的n维球体 Bᵢ(c) 的概率。
  3. 聚合真值：最终的预测分数是对这 N 个模型各自预测的真值进行聚合的结果。论文探索了不同的聚合函数，如min、max和mean。当聚合函数为min时，意味着只有当一个预测在所有 N 个学习到的模型中都具有高置信度时，最终的预测分数才会高。这个过程在计算上模拟了“在所有模型中为真”这一语义蕴含的核心思想。

训练

准备工作与输入数据

在开始训练之前，需要准备好以下四类数据：

1. 蛋白质序列数据：一个包含所有训练蛋白质氨基酸序列的文件。
2. 真实功能注释（Ground Truth Labels）：蛋白质与其对应的GO术语的关联。对于一个包含 M 个GO术语的子本体（如MFO），每个蛋白质的标签是一个 M 维的向量（multi-hot vector） Y_true。如果蛋白质 p 具有第 j 个GO功能，则 Y_true[j] = 1，否则为 0。
3. GO本体文件（Ontology File）：这是包含GO知识库结构的文件，通常是OWL或OBO格式。关键是，它不仅定义了GO术语，还包含了它们之间的逻辑公理（axioms），例如 GO:A ⊑ GO:B（A是B的子类）。

训练循环（Training Loop）中的核心步骤

对于训练集中的每一个数据批次（batch），模型都会执行以下四个步骤：

步骤一：前向传播 (Forward Pass) — 生成预测

1. 序列编码 (Sequence Encoding)：

   • 从批次中取出一个蛋白质 p 的氨基axit序列。
   • 将该序列输入到预训练好且已冻结（frozen）的ESM2模型中。这意味着在训练DeepGO-SE时，ESM2模型的参数是固定不变的，它仅作为特征提取器。
   • ESM2输出一个高维的特征向量 esm2(p)，该向量是对蛋白质序列的浓缩表示。

2. 多模型投影 (Multi-model Projection)：

   • 模型内部有 N 个并行的、结构相同但参数独立的多层感知机（MLPBlock）。
   • 将上一步得到的向量 esm2(p) 同时输入到这 N 个 MLPBlock 中。
   • 每个 MLPBlockᵢ 将 esm2(p) 投影到它自己负责的那个几何表示空间中，生成 N 个不同的蛋白质表示向量：{f₁(p), f₂(p), ..., fₙ(p)}。每一个 fᵢ(p) 都代表蛋白质 p 在第 i 个“可能世界”或“逻辑模型”中的坐标。

3. 多模型评分 (Multi-model Scoring)：

   • 对于子本体中的每一个GO术语 c，模型需要在每一个（共 N 个）几何空间中计算其与蛋白质 p 的关联分数。
   • 在第 i 个模型中，分数 Sᵢ(p, c) 由以下公式计算： Sᵢ(p, c) = σ( dot(fᵢ(p), fᵢ(hF) + fᵢ(c)) + rᵢ(c) )
     • fᵢ(p) 是蛋白质 p 在模型 i 中的向量。
     • fᵢ(c) 和 rᵢ(c) 是GO术语 c 在模型 i 中对应的n维球体的可学习的中心向量和半径。
     • fᵢ(hF) 是“hasFunction”这个关系在模型 i 中的可学习的嵌入向量。
     • dot() 是点积运算，σ 是Sigmoid激活函数，将分数归一化到 (0, 1) 区间，使其具有概率意义。

4. 分数聚合 (Score Aggregation) — 近似语义蕴含：

   • 经过上一步，对于每一个蛋白质-功能对 (p, c)，我们得到了 N 个分数 {S₁(p, c), S₂(p, c), ..., Sₙ(p, c)}。
   • 模型使用一个预定义的聚合函数（如 min, max, 或 mean）将这 N 个分数聚合成一个最终的预测分数 Ŷ(p, c)。例如，如果使用 min 聚合，则 Ŷ(p, c) = min(S₁(p, c), ..., Sₙ(p, c))。
   • 对所有GO术语 c 执行此操作后，得到最终的预测向量 Ŷ，其维度与真实标签 Y_true 相同。

步骤二：损失计算 (Loss Calculation) — 衡量误差

模型的总损失由两个独立的部分加权构成： A. 预测损失 (Prediction Loss, L_pred)

• 目的：衡量模型的预测与真实功能注释之间的差距。
• 计算：使用二元交叉熵损失函数（Binary Cross-Entropy Loss, BCE Loss）。这是处理多标签分类问题的标准损失函数。 L_pred = BCE(Ŷ, Y_true)
• 这个损失会驱动模型学习生成能够匹配真实数据的预测。

B. 几何损失 (Geometric Loss, L_geom)

• 目的：强制模型内部的 N 个几何表示空间遵守GO知识库中的逻辑公理。
• 计算：
  1. 遍历GO本体文件中的每一条公理（例如，'GO:A' ⊑ 'GO:B'）。
  2. 对于每一条公理，在每一个（共 N 个）几何模型中，计算其“违背程度”（violation）。例如，对于公理 'A' ⊑ 'B' 在模型 i 中的违背程度是 max(0, ||cᵢ(A) - cᵢ(B)|| + rᵢ(A) - rᵢ(B))。
  3. L_geom 是所有公理在所有 N 个模型中的违背程度之和。
• 这个损失是一个正则化项，它不关心预测是否准确，只关心模型内部的知识表示是否符合逻辑。

C. 总损失 (Total Loss, L_total)

• 将上述两个损失加权求和： L_total = L_pred + α * L_geom
• α 是一个超参数，用于平衡预测准确性和逻辑一致性的重要性。

ELEmbeddings

看看 ELEmbeddings 是如何实现“GO知识库的几何化表示”的。为了理解ELEmbeddings，我们首先要明确它试图解决的根本问题：

根本问题：神经网络（Neural Networks）的世界是连续的、数字化的（由向量和矩阵构成），而基因本体论（Gene Ontology, GO）这样的知识库是符号化的、离散的（由概念和逻辑规则构成）。这两者之间存在一道鸿沟。我们如何让一个只会做数学计算的神经网络，“理解”并“遵守”像“如果A是B的子类，那么拥有功能A的蛋白质必然拥有功能B”这样的逻辑规则呢？

ELEmbeddings 将逻辑规则翻译成几何关系。

ELEmbeddings 技术讲解

ELEmbeddings 的核心思想可以分解为两个部分：

1. 如何表示一个“概念” (GO术语/Class)？
2. 如何表示它们之间的“逻辑规则” (GO公理/Axiom)？

第一部分：用几何形状表示“概念”

在传统的词嵌入（如Word2Vec）中，一个词被表示为空间中的一个点（一个向量）。但一个点无法表达一个概念的“范围”或“不确定性”。

ELEmbeddings 做了改进：它将每一个GO术语（如“细胞核”、“催化活性”）表示为高维空间中的一个 n维球体 (n-ball)。

一个n维球体由两个参数定义：

1. 中心点向量 (Center vector) c：这个向量捕捉了该概念的核心语义。可以把它想象成这个概念最典型的“意思”。
2. 半径 (Radius) r：这是一个标量值，代表了这个概念的“范围”或“覆盖面”。一个非常宽泛的概念（如“细胞器”）可能会有一个较大的半径，而一个非常具体的概念（如“线粒体内膜”）则会有一个较小的半径。

所以，在ELEmbeddings中：

• “细胞核” 不再是一个点，而是空间中的一个球体 Ball(c_核, r_核)。
• “细胞器” 也是一个球体 Ball(c_器, r_器)。

第二部分：用几何约束表示“逻辑规则”

这是ELEmbeddings最关键的一步。它将GO知识库中的逻辑公理，翻译成了对这些n维球体的位置和大小的几何约束。

我们以GO中最常见、也最重要的一条逻辑规则为例：子类关系 (Subclass of)，记为 C ⊑ D (C是D的子类)。

• 逻辑陈述：'线粒体' ⊑ '细胞器' (线粒体是一种细胞器)。

• 几何翻译：如果“线粒体”是“细胞器”的子类，那么代表“线粒体”的球体，必须完全被代表“细胞器”的球体所包含。

• 如何用数学来表达这个几何约束？ 一个球体A被另一个球体B包含，需要满足一个条件：A的中心点和B的中心点之间的距离，加上A的半径，必须小于或等于B的半径。 用公式表达就是： || c_A - c_B || + r_A ≤ r_B 其中 ||...|| 代表向量的欧几里得距离（即两个中心点之间的直线距离）。

GO知识库中包含成千上万条这样的公理。ELEmbeddings会把每一条公理都转换成类似上述的几何约束方程。例如：

• C ⊑ D -> ||c_C - c_D|| + r_C ≤ r_D
• C ⊓ D ⊑ E (C和D的交集是E的子类) -> 也有对应的、更复杂的几何约束。

如何让神经网络“遵守”这些规则？——通过损失函数

现在我们有了数学化的几何约束，但神经网络在训练开始时，所有这些球体的位置和半径都是随机初始化的，完全不满足这些约束。如何迫使它们在训练过程中逐渐“排列整齐”，最终满足GO的逻辑结构呢？

答案是：设计一个“惩罚”项，即几何损失函数 (Geometric Loss Function)。

1. 定义“违规度” (Violation)：对于每一条公理，比如 '线粒体' ⊑ '细胞器'，模型会计算当前的几何表示“违背”这条规则的程度。 根据上面的公式 ||c_线粒体 - c_细胞器|| + r_线粒体 ≤ r_细胞器，我们可以定义一个“违规度”函数： Loss_axiom = max(0, ||c_线粒体 - c_细胞器|| + r_线粒体 - r_细胞器)

2. 理解这个损失函数：

   • 如果约束被满足：||...|| + r_线粒体 - r_细胞器 的结果将是一个负数或0。那么 max(0, ...) 的结果就是0。这意味着模型没有违反规则，不产生任何惩罚 (Loss=0)。
   • 如果约束被违反：||...|| + r_线粒体 - r_细胞器 的结果将是一个正数。这个正数的大小，就精确地量化了“线粒体”球体“戳出”细胞器球体的程度。这个正数就是惩罚值 (Loss > 0)。

3. 整合到总训练目标中： 模型在训练时，其总的损失函数 (Total Loss) 由两部分组成： Total Loss = Prediction Loss + α * Geometric Loss

   • Prediction Loss：这是标准的监督学习损失，用于衡量模型的预测与真实标签之间的差距（例如使用交叉熵损失）。它驱使模型做出准确的预测。
   • Geometric Loss：这是所有GO公理产生的“违规度”惩罚的总和。它驱使模型调整所有n维球体的中心点 c 和半径 r，使得它们之间的几何关系尽可能地满足整个GO知识库的逻辑结构。
   • α 是一个超参数，用于平衡这两个目标的重要性。

训练过程就像一个双重任务：模型一方面要努力学习如何正确预测蛋白质功能（最小化Prediction Loss），另一方面，它必须在“整理”内部的几何知识库，让所有概念球体各就其位，遵守逻辑规则（最小化Geometric Loss）。

经过训练后，ELEmbeddings为我们创造了一个结构化的、语义丰富的向量空间。在这个空间里：

• 向量（球体的中心）的位置不再是任意的，它们的相对位置和包含关系反映了GO的内在逻辑。
• 当DeepGO-SE模型将一个蛋白质的ESM2向量投影到这个空间时，它实际上是在这个已经“懂”了生物学逻辑的坐标系中为该蛋白质寻找一个定位。如果蛋白质的向量落在了“线粒体”球体内，那么根据“真路径规则”（True Path Rule），它也必然位于“细胞器”球体内。这样，模型的预测就天然地具有了逻辑一致性。