1 PatchTST

论文名称：A Time Series is Worth 64 Words: Long-term Forecasting with Transformers
论文地址：https://arxiv.org/abs/2211.14730 (opens new window)
引用量（截止到2025.07.08）：2169
Venue：ICLR 2023
代码开源地址：https://github.com/yuqinie98/PatchTST (opens new window) Star 数：2100+

2 一句话总结这篇论文

这篇论文主要提出了将序列分 patch 、一个变量一个通道和自监督训练（“完形填空”）。

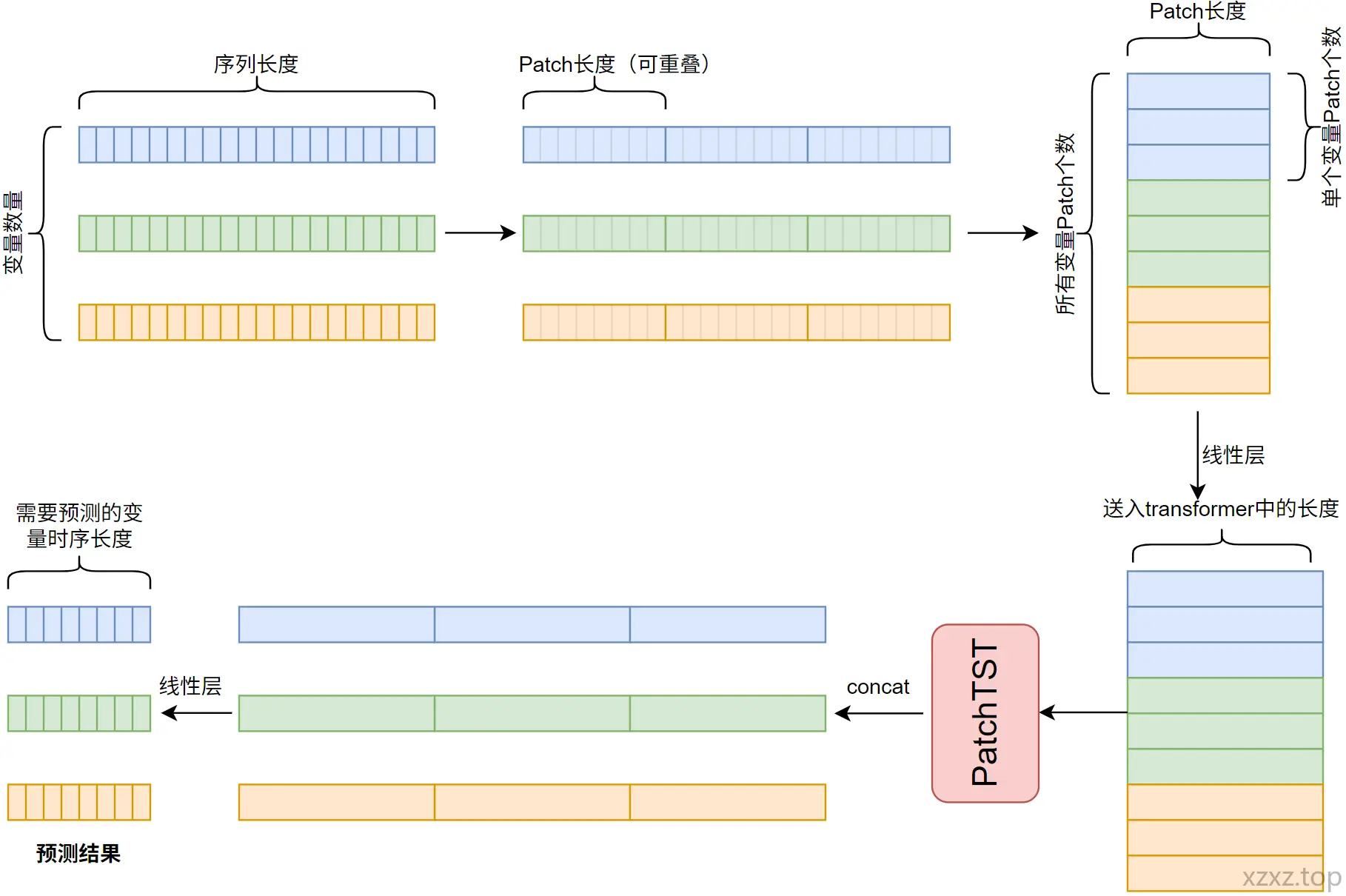
上图为我根据它的代码画的更详细的数据流向图。

3 摘要

本文提出了一种高效的基于 Transformer 的多变量时间序列预测与自监督表示学习模型设计。该方法基于两个关键组件：（i）将时间序列划分为子序列级别的 patch，并作为 Transformer 的输入 token；（ii）通道独立性，即每个通道包含一个单变量时间序列，所有通道共享相同的嵌入层和 Transformer 权重。patch 的设计带来了三重优势：保留局部语义信息；在相同的历史窗口下显著降低 attention 图的计算和内存开销（为平方级别的降低）；模型能够关注更长的历史序列。本文提出的通道独立 patch 时间序列 Transformer（PatchTST）在长期预测准确性上显著优于当前最先进的 Transformer 模型。本文还将该模型应用于自监督预训练任务，并在微调时取得了优异表现，甚至在大型数据集上超过了有监督训练的效果。将预训练的掩码表示从一个数据集迁移到其他数据集，也能实现当前最优的预测准确率。

4 引言

预测是时间序列分析中最重要的任务之一。随着深度学习模型的快速发展，该领域的研究工作数量显著增加。深度模型不仅在预测任务中表现出色，还在表示学习中展现了强大的能力，能够提取抽象表示并迁移到分类、异常检测等多种下游任务中，达到当前最先进（SOTA） 的效果。

在众多深度学习模型中，Transformer 在自然语言处理（NLP）、计算机视觉（CV）、语音等多个应用领域取得了巨大成功，其注意力机制能够自动学习序列中各元素之间的依赖关系，因此非常适合用于序列建模任务。近年来，Transformer 也逐渐被应用到时间序列建模中，代表性模型包括 Informer、Autoformer 和 FEDformer。然而，尽管这些 Transformer 变体设计复杂，一项最新研究表明，一个非常简单的线性模型在多个常用基准任务上却能超越所有这些模型的性能，从而对 Transformer 在时间序列预测中的有效性提出了质疑。

本文尝试通过提出一种 通道独立 patch 时间序列 Transformer 模型（PatchTST） 来回答这一问题。该模型包含两个关键设计：

• Patching（分块）：时间序列预测的核心目标是理解不同时间步之间的相关性。然而，单个时间步并不像句子中的一个词那样具有语义意义，因此提取局部语义信息对于分析时间序列的内部关联至关重要。大多数已有方法仅使用逐点（point-wise）输入 token，或依赖于手工设计的信息表示。相比之下，我们通过将时间步聚合成子序列级别的 patch，不仅增强了局部性，还捕捉到了在逐点层面无法获取的丰富语义信息。
• 通道独立性（Channel-independence）：一个多变量时间序列本质上是一个多通道信号，每个 Transformer 输入 token 可以包含来自单个通道或多个通道的数据。不同的输入 token 设计对应着 Transformer 架构的不同变体。“通道混合”（channel-mixing）指的是输入 token 包含所有时间序列通道的向量，并投影到嵌入空间以进行信息混合。相对地，“通道独立”表示每个输入 token 仅包含来自一个通道的信息。这一策略已在 CNN 和线性模型中被验证有效，但此前尚未被应用于基于 Transformer 的模型中。

PatchTST 正是结合了以上两种设计，兼顾局部语义表达与通道结构解耦的优势，从而推动 Transformer 在时间序列建模上的性能极限。

我们在表 1 中通过对 Traffic 数据集进行案例研究展示了模型的关键结果，该数据集包含 862 条时间序列。我们的模型具有以下几个优势：

1. 时间与空间复杂度的降低：原始的 Transformer 在时间和空间上的复杂度为 $O(N^2)$，其中 $N$ 是输入 token 的数量。在没有预处理的情况下，$N$ 通常等于输入序列长度 $L$，这在实践中成为计算和内存的主要瓶颈。通过应用 patching，可以将 $N$ 减少一个与步幅相关的因子：$N \approx L/S$，从而使复杂度以平方级别降低。表 1 展示了 patching 的优势。当设定 patch 长度 $P = 16$、步幅 $S = 8$，且 $L = 336$ 时，在大规模数据集上训练时间最多可缩短至原来的 1/22。

2. 利用更长历史窗口的能力：表 1 显示，当将 look-back window $L$ 从 96 增加到 336 时，MSE 从 0.518 降低到 0.397。然而，简单地扩展 $L$ 会增加内存和计算资源的使用。由于时间序列通常存在大量时间冗余信息，已有研究尝试通过下采样或设计稀疏 attention 结构来丢弃部分数据点，模型依然能获取足够信息完成预测。我们进一步研究了 $L = 380$ 的情形，其中时间序列每 4 步采样一次，并在序列末尾补上最后一个点，使得最终的输入 token 数为 $N = 96$。这种设置下的 MSE 为 0.447，优于仅使用最近 96 个时间步（MSE = 0.518）的情形。这表明在输入 token 数量相同的前提下，较长的历史窗口包含了更有用的信息。这引发一个问题：有没有办法在不舍弃数据点的情况下使用长窗口？Patching 是一个很好的答案。它可以对局部时间步进行聚合，从而既保留信息，又减少输入 token 长度，达到降低计算复杂度的目的。如表 1 所示，当 $L = 336$ 时，使用 patching 后 MSE 进一步从 0.397 降低到 0.367。

3. 表示学习能力：随着强大的自监督学习技术的兴起，模型需要具备复杂的非线性结构来捕捉数据的抽象表示。像线性模型这类简单结构由于表达能力有限，可能并不适合这种任务。通过我们提出的 PatchTST 模型，我们不仅验证了 Transformer 在时间序列预测中的有效性，还展示了其强大的表示能力可以进一步提升预测性能。我们的 PatchTST 在表 1 中获得了最好的 MSE（0.349）。

我们将在接下来的章节中更详细地介绍我们的方法，并进行大量实验证明我们的论点。我们不仅通过有监督的预测结果和消融实验展示了模型的有效性，还达到了当前最先进（SOTA）的自监督表示学习和迁移学习性能。

表 1：这是在 Traffic 数据集上进行的多变量时间序列预测案例研究，预测步长为 96。表中展示了在不同回溯窗口 $L$ 和输入 token 数量 $N$ 下的结果。最佳结果以加粗形式标出，次优结果以下划线标出。其中，down-sampled 指的是每隔 4 步采样一次并补上最后一个值的策略。所有结果均来自监督训练，除最佳结果外，该结果使用的是自监督学习。

5 相关工作

5.1 Transformer 中的 patch 技术

Transformer 已在多种数据模态上展现出显著的潜力。在诸多应用中，patching 是一种在局部语义信息重要时不可或缺的设计。在自然语言处理中，BERT 采用子词级（subword-based）分词方法，而非基于字符的方式。在计算机视觉领域，Vision Transformer（ViT）是一个里程碑式的工作，其将图像划分为 $16 \times 16$ 的 patch 后输入到 Transformer 模型中。后续的一些重要工作如 BEiT 和 Masked Autoencoders 也都采用 patch 作为输入。同样，在语音研究中，研究人员使用卷积方法从原始音频输入中提取子序列级别的信息。

5.2 基于 Transformer 的长期时间序列预测

近年来，已有大量研究尝试将 Transformer 模型应用于长期时间序列预测。我们在此总结其中一些代表性工作。LogTrans 使用带有 LogSparse 结构的卷积式自注意力机制以捕捉局部信息并降低空间复杂度。Informer 提出了 ProbSparse 自注意力机制，结合蒸馏技术高效地提取最关键的键值。Autoformer 借鉴了传统时间序列分析中的分解和自相关思想。FEDformer 利用傅里叶增强结构实现线性复杂度。Pyraformer 则引入金字塔注意力模块，融合了尺度间与尺度内的连接，也实现了线性复杂度。

这些模型大多聚焦于设计新颖的机制来减少原始注意力机制的复杂度，以在预测长度较长时提升预测性能。然而，它们大多仍采用点级（point-wise）的注意力，即以单一时间步的数据为基础计算 key-query 的点积。例如，LogTrans 避免了逐点的点积操作，但其值仍基于单个时间步；Autoformer 使用自相关来获取 patch 级别的连接，但其方式为手工设计，不能全面包含 patch 中的语义信息；Triformer 提出 patch attention，其目的是通过在 patch 内部使用伪时间戳作为 query 来降低复杂度，但这种方法既没有将 patch 视作一个基本输入单元，也未揭示 patch 中的语义重要性。

5.3 时间序列表示学习

除了监督学习，自监督学习也是时间序列建模中的一个重要研究方向，因为其已经展现出在学习可迁移表示方面的巨大潜力。近年来，已经有许多非 Transformer 的模型被提出用于时间序列表示学习。同时，Transformer 被认为是构建通用基础模型和学习通用表示的理想选择。虽然已有研究尝试将 Transformer 应用于时间序列表示学习，例如 Time Series Transformer（TST）和 TS-TCC，但目前 Transformer 在该领域的潜力尚未被充分挖掘。

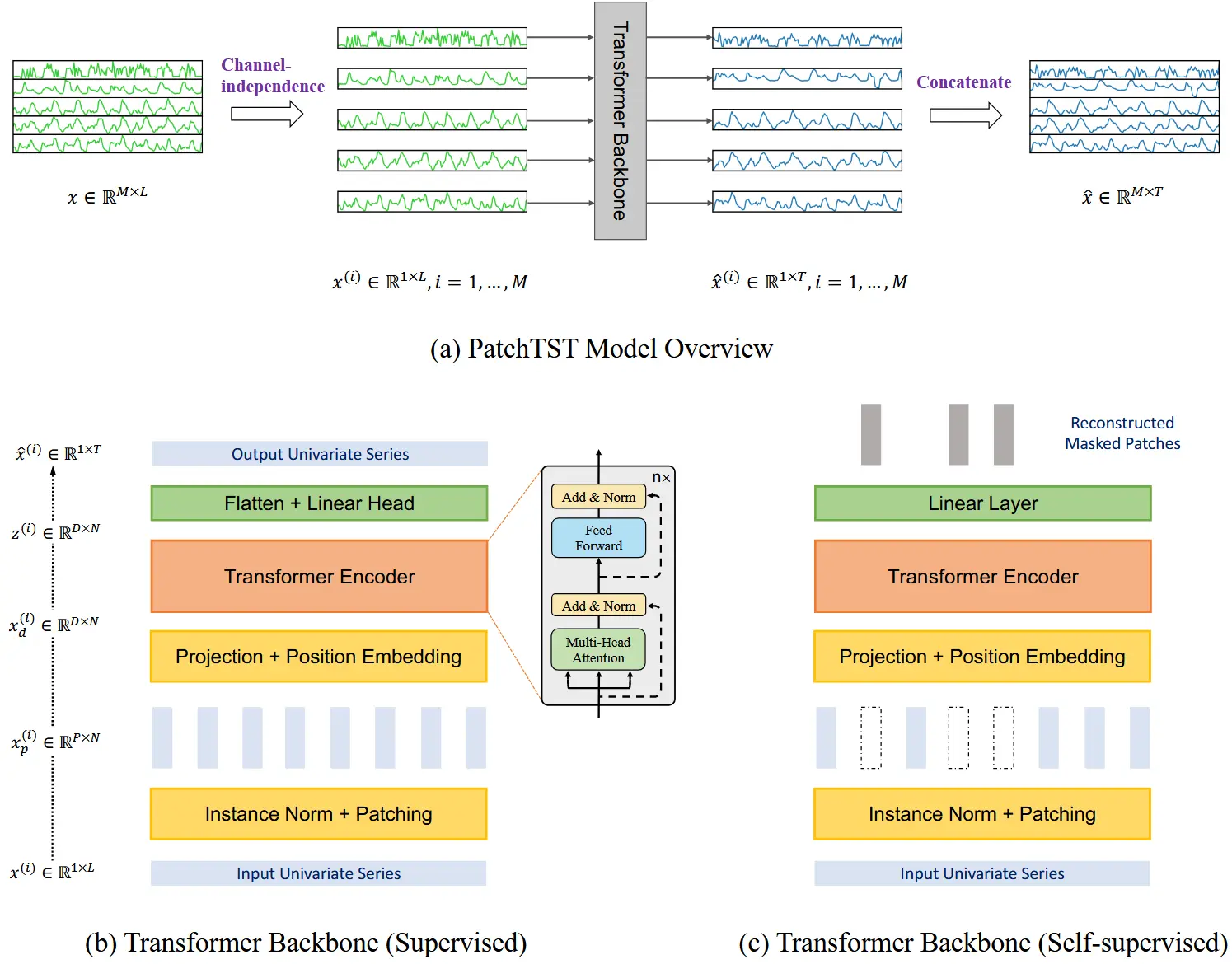
图 1：PatchTST 架构。(a) 多变量时间序列数据被划分为不同的通道。各通道共享相同的 Transformer 主干网络，但其前向过程是彼此独立的。(b) 每个通道的单变量序列首先通过实例归一化操作，并被划分为若干 patch。这些 patch 被用作 Transformer 的输入 token。(c) PatchTST 的掩码式自监督表示学习，其中 patch 被随机选中并置为零，模型需要重建这些被遮蔽的 patch。

6 方法介绍

6.1 模型结构

我们考虑如下问题：给定一组多变量时间序列样本，输入窗口长度为 $L$，记为 $(x_1, ..., x_L)$，其中每个时间步 $x_t$ 是维度为 $M$ 的向量，我们希望预测接下来的 $T$ 个时间步的值，即 $(x_{L+1}, ..., x_{L+T})$。我们提出的 PatchTST 如图 1 所示，模型的核心架构是 vanilla Transformer 编码器。

6.1.1 前向过程

我们将第 $i$ 个长度为 $L$ 的单变量时间序列表示为：

$$x_{1:L}^{(i)} = \left(x_1^{(i)}, \dots, x_L^{(i)}\right)$$

其中 $i = 1, ..., M$，输入序列 $(x_1, ..., x_L)$ 被拆分为 $M$ 条单变量时间序列 $x^{(i)} \in \mathbb{R}^{1 \times L}$，每一条都独立地输入 Transformer 主干网络，符合我们提出的“通道独立性”设计。Transformer 主干随后为每条时间序列提供预测结果：

$$\hat{x}^{(i)} = \left(\hat{x}_{L+1}^{(i)}, \dots, \hat{x}_{L+T}^{(i)}\right) \in \mathbb{R}^{1 \times T}$$

6.1.2 前向过程更详细解释

非常好，我们来详细解释一下这段内容，特别是 PatchTST 中模型输入的形式和“通道独立性”是如何工作的。

问题背景（你要做什么）

我们要解决的问题是： 给定一段历史的多变量时间序列，预测它未来的多个时间点的值。 具体地说：

• 输入：一段长度为 $L$ 的多变量时间序列，记为 $(x_1, x_2, ..., x_L)$
• 其中每个 $x_t \in \mathbb{R}^M$，表示在时间点 $t$ 的一个 $M$ 维向量，也就是这个时间点上有 $M$ 个变量（或通道）的观测值
• 输出：希望预测接下来的 $T$ 个时间点的值，即 $(x_{L+1}, ..., x_{L+T})$

输入拆分与“通道独立性”

我们将输入的时间序列按照通道（变量）来“拆分”：

• 每个通道表示一个变量在所有时间点上的变化趋势，比如第 $i$ 个通道可以表示“温度”或“交通流量”等。
• 第 $i$ 条通道（也就是第 $i$ 个变量）可以表示为一条单变量时间序列：

$$x^{(i)}_{1:L} = \left(x^{(i)}_1, x^{(i)}_2, ..., x^{(i)}_L\right) \in \mathbb{R}^{1 \times L}$$

也就是一个长度为 $L$ 的序列，只包含一个通道。 这样，原始的 $L \times M$ 的多变量时间序列就被拆分成了 $M$ 条 $1 \times L$ 的序列。

通道独立性（Channel-Independence）

PatchTST 的一个关键设计是：每个通道的序列都独立地送入 Transformer 模型中做处理，而不是像传统 Transformer 那样把所有通道拼在一起后一起处理。

• 所有通道共用一套 Transformer 模型（同样的权重），但每个通道单独前向传播。
• 这样每个通道都拥有自己独立的建模路径，避免了不同通道之间的干扰，也节省了计算资源。

最终，每个通道得到的预测结果为：

$$\hat{x}^{(i)} = \left(\hat{x}^{(i)}_{L+1}, \hat{x}^{(i)}_{L+2}, ..., \hat{x}^{(i)}_{L+T}\right) \in \mathbb{R}^{1 \times T}$$

也就是说，对第 $i$ 个通道，我们预测了未来 $T$ 个时间点的值。

举个例子帮忙理解

假设：

• 我们有一个 3 通道的时间序列（比如温度、湿度、风速）
• 每条通道有过去 100 步的历史数据，也就是 $L = 100$
• 我们要预测未来 24 步，也就是 $T = 24$

PatchTST 做的事是：

1. 把 3 条通道分别抽出来，得到：
   • 温度的长度为 100 的序列 $x^{(1)}$
   • 湿度的序列 $x^{(2)}$
   • 风速的序列 $x^{(3)}$
2. 把这三条序列分别输入 Transformer 模型（用的是同一个模型），得到它们各自未来 24 步的预测值
3. 最终得到三个序列的预测结果 $\hat{x}^{(1)}, \hat{x}^{(2)}, \hat{x}^{(3)}$

6.1.3 Patching（分块）

每个输入的单变量时间序列 $x^{(i)}$ 会首先被划分为一系列 patch，这些 patch 可以是重叠的，也可以是不重叠的。设定 patch 长度为 $P$，步幅（即两个相邻 patch 之间的不重叠区域）为 $S$，那么分块过程会生成如下形式的一组 patch：

$$x_p^{(i)} \in \mathbb{R}^{P \times N}$$

其中 $N$ 是 patch 的个数，计算公式为：

$$N = \left\lfloor \frac{L - P}{S} \right\rfloor + 2$$

在实际处理前，我们会在原始序列末尾补上 $S$ 个重复的最后一个数值 $x_L^{(i)} \in \mathbb{R}$。补 S 个最后的值是为了防止最后一个 patch 越界，保证 patch 数量是固定的，并且能利用序列尾部的关键信息。

使用 patch 后，输入 token 的数量可由原始的 $L$ 减少为约 $L / S$。这意味着注意力图的内存消耗和计算复杂度可以按因子 $S$ 的平方量级降低。因此，在训练时间和 GPU 内存受限的情况下，patch 设计可以让模型看到更长的历史序列，从而显著提升预测性能，正如表 1 中所展示的那样。

6.1.4 Transformer 编码器

我们使用标准的 Transformer 编码器，将观测到的信号映射到潜在表示空间。每个 patch 被映射到维度为 $D$ 的 Transformer 潜在空间中，映射方式为一个可训练的线性投影矩阵：

$$\mathbf{W}_p \in \mathbb{R}^{D \times P}$$

并加上一个可学习的位置编码：

$$\mathbf{W}_{\text{pos}} \in \mathbb{R}^{D \times N}$$

以用于标识 patch 的时间顺序。因此，patch 的最终表示为：

$$\mathbf{x}_d^{(i)} = \mathbf{W}_p \mathbf{x}_p^{(i)} + \mathbf{W}_{\text{pos}} \in \mathbb{R}^{D \times N}$$

该表示将作为输入送入图 1 所示的 Transformer 编码器。接着，多头注意力机制中的每一个头（$h = 1, ..., H$）会将其输入转换为：Query 查询矩阵：$\mathbf{Q}_h^{(i)} = (\mathbf{x}_d^{(i)})^\top \mathbf{W}_h^Q$， Key 键矩阵：$\mathbf{K}_h^{(i)} = (\mathbf{x}_d^{(i)})^\top \mathbf{W}_h^K$，Value 值矩阵：$\mathbf{V}_h^{(i)} = (\mathbf{x}_d^{(i)})^\top \mathbf{W}_h^V$，其中：$\mathbf{W}_h^Q, \mathbf{W}_h^K \in \mathbb{R}^{D \times d_k}$， $\mathbf{W}_h^V \in \mathbb{R}^{D \times D}$。之后，通过缩放点积注意力计算得到每个头的输出：

$$(\mathbf{O}_h^{(i)})^\top = \text{Attention}(\mathbf{Q}_h^{(i)}, \mathbf{K}_h^{(i)}, \mathbf{V}_h^{(i)}) = \text{Softmax}\left(\frac{\mathbf{Q}_h^{(i)} (\mathbf{K}_h^{(i)})^\top}{\sqrt{d_k}}\right) \mathbf{V}_h^{(i)}$$

其中 $\mathbf{O}_h^{(i)} \in \mathbb{R}^{D \times N}$。多头注意力模块还包括 BatchNorm 层和带有残差连接的前馈神经网络（如图 1 所示）。最终，模型输出的表示为：

$$\mathbf{z}^{(i)} \in \mathbb{R}^{D \times N}$$

然后，使用 flatten 操作和线性投影层，将该表示映射为预测结果：

$$\hat{x}^{(i)} = (\hat{x}_{L+1}^{(i)}, \dots, \hat{x}_{L+T}^{(i)}) \in \mathbb{R}^{1 \times T}$$

6.1.5 损失函数（Loss Function）

我们选择使用均方误差（MSE）损失来衡量预测值与真实值之间的差异。每个通道的损失会被分别计算，并在 $M$ 条时间序列上取平均，得到整体目标函数如下：

$$\mathcal{L} = \mathbb{E}_x \left[\frac{1}{M} \sum_{i=1}^{M} \left\| \hat{x}^{(i)}_{L+1:L+T} - x^{(i)}_{L+1:L+T} \right\|_2^2 \right]$$

6.1.6 实例归一化（Instance Normalization）

该技术最近被提出，用于缓解训练数据与测试数据之间的分布漂移问题。具体来说，它会将每条时间序列 $x^{(i)}$ 做零均值、单位方差的归一化处理。在操作上，我们在 patching 之前对每个 $x^{(i)}$ 进行归一化处理，预测输出时再将原始的均值和标准差加回去。

6.2 表示学习（Representation Learning）

自监督表示学习已成为从未标注数据中提取高层抽象表示的热门方法。在本节中，我们将 PatchTST 应用于多变量时间序列的自监督表示学习，并展示所学表示在预测任务中的有效迁移能力。

在自监督预训练中，最常见的方法之一是掩码自编码器（masked autoencoder），该方法已在 NLP 和 CV 等领域成功应用。其思想很简单：随机地遮蔽输入序列的一部分，并训练模型去还原被遮蔽的内容。

掩码编码器也已被引入时间序列建模，并在分类和回归任务中取得了显著效果。某些方法将多变量时间序列输入到 Transformer 中，其中每个输入 token 是在第 $i$ 个时间步的时间序列向量 $x_i$。mask 操作会在每条时间序列和跨序列中随机执行。然而，这种做法存在两个潜在问题：

1. 遮蔽是作用在单个时间步上。当前时间步被遮蔽的值可能可以通过插值其前后值直接推断出来，而不需要对整个序列进行高级理解，这背离了我们希望学习整体信号抽象表示的目标。一些研究者尝试引入更复杂的随机策略，例如对不同长度的时间序列分组并随机遮蔽。

2. 用于预测任务的输出层设计复杂。假设每个时间步的表示为 $\mathbf{z}_t \in \mathbb{R}^D$，则所有 $L$ 个时间步构成的表示将通过一个线性映射输出至目标结果，其形状为 $M$ 个变量，每个变量有 $T$ 个预测时间点。这样需要一个维度为 $(L \cdot D) \times (M \cdot T)$ 的参数矩阵 $\mathbf{W}$。当 $L$、$D$、$M$、$T$ 中任意一个值较大时，该矩阵将变得非常庞大，容易导致过拟合，特别是在下游训练样本数量较少的情况下。

我们提出的 PatchTST 可以自然地解决上述问题。如图 1 所示，我们在自监督设置中仍然使用与有监督相同的 Transformer 编码器结构，但去除了预测头，并添加了一个 $D \times P$ 的线性层。

与有监督模型中允许 patch 之间重叠不同，在自监督预训练中，我们将每条输入序列划分为规则的非重叠 patch，这样做的目的是确保观测到的 patch 不会包含被遮蔽 patch 的信息。随后，我们从所有 patch 的索引中随机均匀选取一部分进行遮蔽，将这些选中的 patch 用零值替换。模型使用 MSE 损失函数训练，以重建这些被遮蔽的 patch。

我们特别强调：每条时间序列将拥有自己的潜在表示，这些表示通过共享权重机制进行交叉学习。该设计允许预训练数据中包含与下游任务中不同数量的时间序列，这在其他方法中可能难以实现。

6.2.1 模型变体（Model Variants）

我们提出了两种版本的 PatchTST：

• PatchTST/64：表示输入 patch 的数量为 64，对应的回溯窗口（look-back window）为 $L = 512$；
• PatchTST/42：表示输入 patch 的数量为 42，使用默认的回溯窗口 $L = 336$。

这两个版本都采用 patch 长度 $P = 16$、步幅 $S = 8$。因此，PatchTST/42 可用于与 DLinear 及其他基于 Transformer 的模型做公平比较，而 PatchTST/64 则可用于在更大规模数据集上进一步探索更优性能。更多实验细节见附录 A.1。