Pyraformer

论文名称：Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting
中文名称：Pyraformer：用于长距离时间序列建模与预测的低复杂度金字塔注意力机制 论文地址：https://repositum.tuwien.at/handle/20.500.12708/135874 (opens new window)
引用量（截止到2025.07.08）：1068
Venue：ICLR 2022

一句话总结这篇论文

Pyraformer 使用了 1D 卷积初始化金字塔图中粗尺度的节点，在提出的金字塔注意力模块中，一个节点最多只会关注 $A + C + 1$ 个节点（A 表示兄弟节点数量，C表示子节点数量，1表示父节点）。

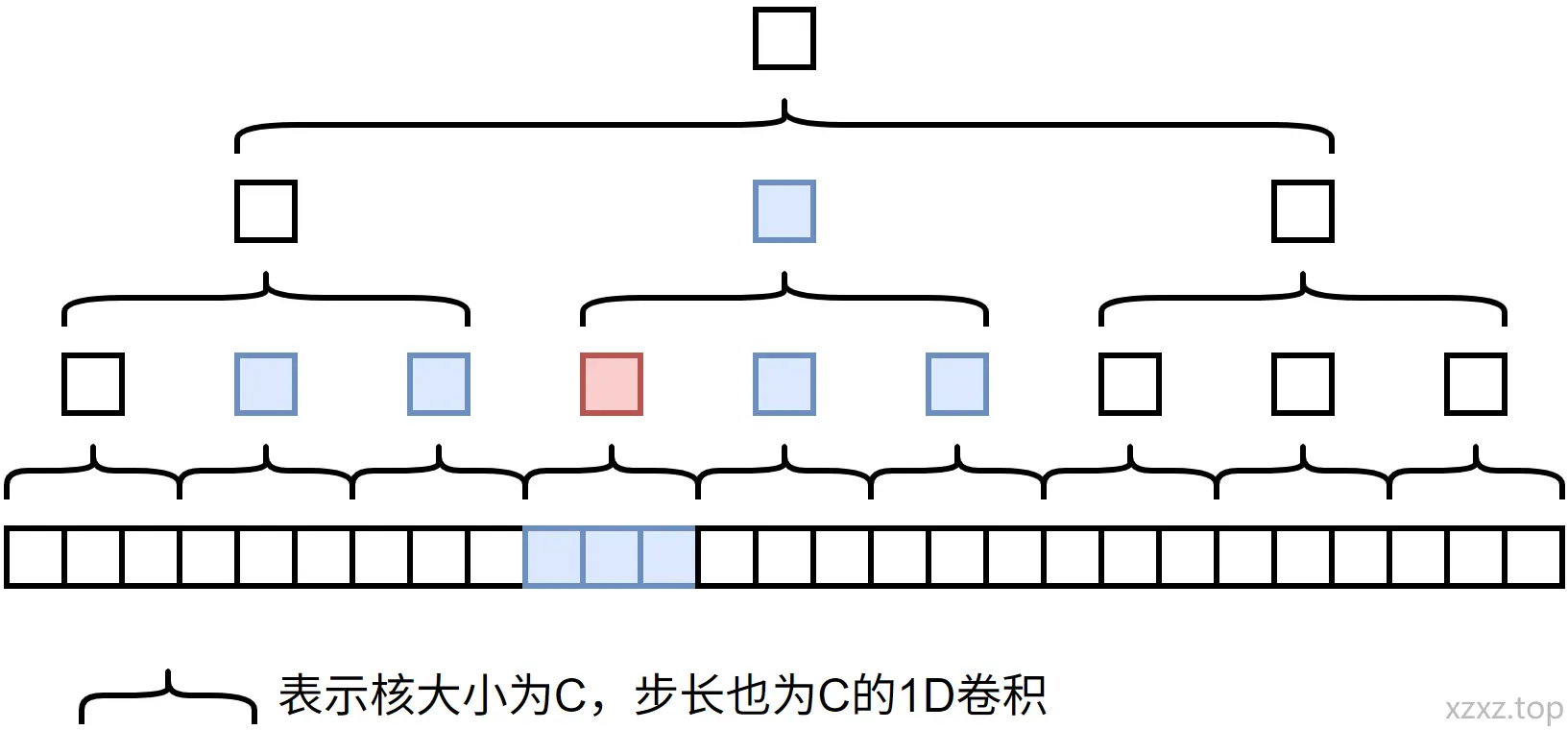
为更好理解 Pyraformer 的核心思想，以 C 为 3 为例画了一个示意图。首先 Pyraformer 会使用1D 的卷积初始化一个金字塔特征，后续将在这个金字塔特征上进行计算注意力，假如要更新红色的节点，选取三种局部特征：子节点、兄弟节点、父节点，用这三种特征更新自己。

摘要

基于时间序列数据，利用过去准确预测未来具有极其重要的意义，因为这为提前进行决策和风险管理提供了可能。在实际应用中，挑战在于构建一个既灵活又简洁的模型，能够捕捉广泛的时间依赖关系。本文提出了 Pyraformer，通过探索时间序列的多分辨率表示来实现建模。具体而言，本文引入了金字塔注意力模块（Pyramidal Attention Module, PAM），其中跨尺度的树状结构用于汇总不同分辨率下的特征，而同尺度的邻接连接则用于建模不同范围的时间依赖关系。在温和的条件下，Pyraformer 中信号传递路径的最大长度相对于序列长度 L 是常数（即 O(1)），而其时间和空间复杂度则随 L 线性增长。大量实验结果表明，Pyraformer 在单步预测和长距离多步预测任务中通常能够以最少的时间和内存消耗，尤其是在序列较长的情况下，达到最高的预测准确率。

引言

时间序列预测是下游任务（如决策制定和风险管理）的基石。例如，微服务的在线流量若能被可靠地预测，就可以为云系统中的潜在风险提供早期预警。此外，它还能为动态资源分配提供指导，从而在不降低性能的前提下最小化成本。除了在线流量预测，时间序列预测还被广泛应用于其他领域，包括疾病传播、能源管理、经济与金融等。

时间序列预测的主要挑战在于构建一个既强大又简洁的模型，能够紧凑地捕捉不同范围的时间依赖关系。时间序列通常同时包含短期和长期的重复模式，考虑这些模式是实现准确预测的关键。特别值得注意的是，处理长距离依赖关系的任务更为困难，其难点体现在时间序列中任意两个位置之间的最长信号传递路径的长度（见命题 2 的定义）。该路径越短，依赖关系的捕捉效果越好。此外，为了让模型学习这些长期模式，输入的历史序列也应足够长。因此，低时间和空间复杂度成为优先考虑的因素。

不幸的是，目前的先进方法尚无法同时满足这两个目标。一方面，RNN 和 CNN 在时间复杂度方面具有线性优势（即 $O(L)$，其中 $L$ 为时间序列长度），但它们的最长信号传递路径也是 $O(L)$，这使得它们难以学习远距离位置之间的依赖关系。另一方面，Transformer 将最大路径显著缩短为 $O(1)$，但代价是时间复杂度上升为 $O(L^2)$，从而难以处理非常长的序列。为了在模型能力和复杂度之间寻求折中，研究者提出了多种 Transformer 的变体，如 Longformer、Reformer 和 Informer。然而，这些方法中很少能在将最大路径长度缩短至小于 $O(L)$ 的同时，大幅降低时间和空间复杂度。

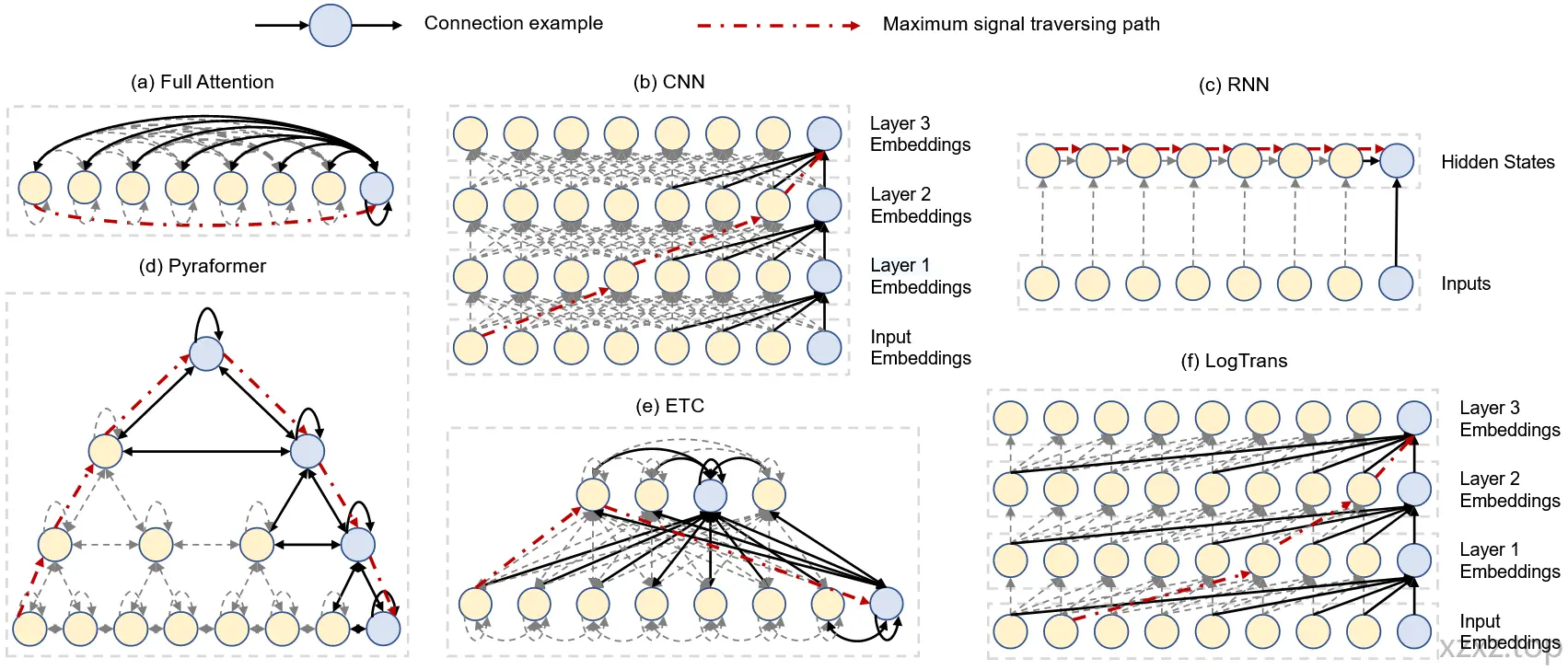
图 1：常用神经网络序列建模方法的图结构表示。

本文提出了一种基于金字塔注意力机制的新型 Transformer 模型 —— Pyraformer，旨在填补捕捉长距离依赖关系与实现低时间和空间复杂度之间的鸿沟。具体而言，我们构建了金字塔注意力机制，通过在图结构中基于注意力的消息传递（见图 1(d)）来实现。

该图中的边可分为两类：跨尺度连接（inter-scale） 与同尺度连接（intra-scale）。

• 跨尺度连接用于构建原始序列的多分辨率表示：最细尺度的节点对应原始时间序列中的时间点（例如每小时观测值），而更粗尺度的节点则表示低分辨率的特征（例如每日、每周或每月的模式）。这些隐含的粗尺度节点最初是通过一个粗尺度构造模块引入的。
• 同尺度连接则通过连接相邻节点，捕捉每一分辨率下的时间依赖关系。

通过这种设计，模型能以紧凑的形式在较粗尺度上捕捉长距离的时间依赖，从而缩短信号传递路径的长度。此外，在不同尺度上使用稀疏的同尺度邻接连接建模不同范围的时间依赖，也能显著降低计算成本。简而言之，本文的主要贡献包括：

• 我们提出了 Pyraformer，用紧凑的多分辨率结构同时捕捉不同范围的时间依赖关系。为突出其区别于现有方法，我们从图结构的角度对所有模型进行了归纳总结（见图 1）。
• 从理论上证明：通过适当选择参数，Pyraformer 可同时实现最大路径长度为 $O(1)$，以及时间与空间复杂度为 $O(L)$。
• 从实验上验证：在多个真实世界的数据集上，Pyraformer 在单步预测与长距离多步预测任务中均取得比原始 Transformer 及其变体更高的预测准确率，同时耗时与内存占用更低。

相关工作

时间序列预测

时间序列预测方法大致可分为统计方法与基于神经网络的方法。第一类包括 ARIMA 和 Prophet 等模型。然而，这些方法通常需要对每一个时间序列分别建模，在处理长距离预测时性能较差。

近年来，深度学习的发展带来了大量基于神经网络的时间序列预测方法，包括 CNN、RNN 和 Transformer。如前所述，CNN 和 RNN 拥有较低的时间与空间复杂度（即 $O(L)$），但在建模长距离依赖关系时，其信号传递路径长度为 $O(L)$，使其难以捕捉远距离位置之间的关系。关于相关的 RNN 模型，读者可参考附录 A 的详细回顾。

相较之下，Transformer 能够以仅 $O(1)$ 的路径长度有效捕捉长距离依赖，但其计算复杂度从 $O(L)$ 急剧上升至 $O(L^2)$。为缓解这种计算负担，研究者提出了 LogTrans 和 Informer 两种变体：

• LogTrans 约束序列中每个点只能关注其前面距离为 $2^n$ 的点（其中 $n = 1, 2, \cdots$），从而稀疏化了注意力结构；
• Informer 则利用注意力分数的稀疏性，大幅降低了复杂度（达到 $O(L \log L)$），但代价是引入了更长的最大路径长度。

稀疏 Transformer

除了时间序列预测领域，在自然语言处理（NLP）中也涌现出大量旨在提高 Transformer 效率的方法。与 CNN 类似，Longformer 采用局部滑动窗口或扩张滑动窗口内的注意力机制。尽管其计算复杂度被降低为 $O(AL)$（其中 $A$ 为窗口大小），但由于窗口有限，使得全局信息交换变得困难，从而使最大路径长度为 $O(L/A)$。

作为替代方案，Reformer 利用局部敏感哈希（LSH） 将序列划分为若干桶，并仅在桶内执行注意力计算。同时，它还采用可逆 Transformer 结构进一步降低内存消耗，从而能够处理非常长的序列。然而，它的最大路径长度与桶的数量成正比，更糟糕的是，为了降低复杂度，需要引入大量的桶。

另一方面，ETC 引入一组额外的全局 token以实现全局信息交互，使其时间和空间复杂度达到 $O(GL)$，最大路径长度为 $O(1)$，其中 $G$ 为全局 token 的数量。但由于 $G$ 通常随着 $L$ 的增长而增加，因此其总体复杂度仍然是超线性的。

类似于 ETC，本文提出的 Pyraformer 也引入了全局 token，但采用了多尺度方式，在不增加最大路径长度的情况下，将复杂度成功降低至 $O(L)$，优于原始 Transformer 的 $O(L^2)$。

分层 Transformer

最后，我们简要回顾一些用于提升 Transformer 建模自然语言层次结构能力的方法，尽管这些方法尚未被应用于时间序列预测。

HIBERT 首先使用句子编码器（Sent Encoder）提取每个句子的特征，然后将文档中各句的结束标记（EOS token）组成新的序列，输入到文档编码器（Doc Encoder）中。然而，该方法专门面向自然语言，无法推广到其他类型的序列数据。

Multi-scale Transformer 则通过自顶向下与自底向上的网络结构，学习序列数据的多尺度表示。这种多尺度表示有助于降低原始 Transformer 的时间与内存开销，但仍受限于其二次复杂度（$O(L^2)$）。

作为另一种替代，BP-Transformer 采用递归二分方式将整个输入序列划分，直到每个片段只包含一个 token。划分后的片段构成一棵二叉树。在注意力层中，每个上层节点可以关注其子节点，而最底层的节点可以关注同一层中相邻的 $A$ 个节点以及所有更高层的节点。需要注意的是，BP-Transformer 将粗尺度节点初始化为全零，而 **Pyraformer 则通过结构模块灵活构建这些节点。

此外，BP-Transformer 所对应的图结构比 Pyraformer 更密集，因此其复杂度较高，达到 $O(L \log L)$。

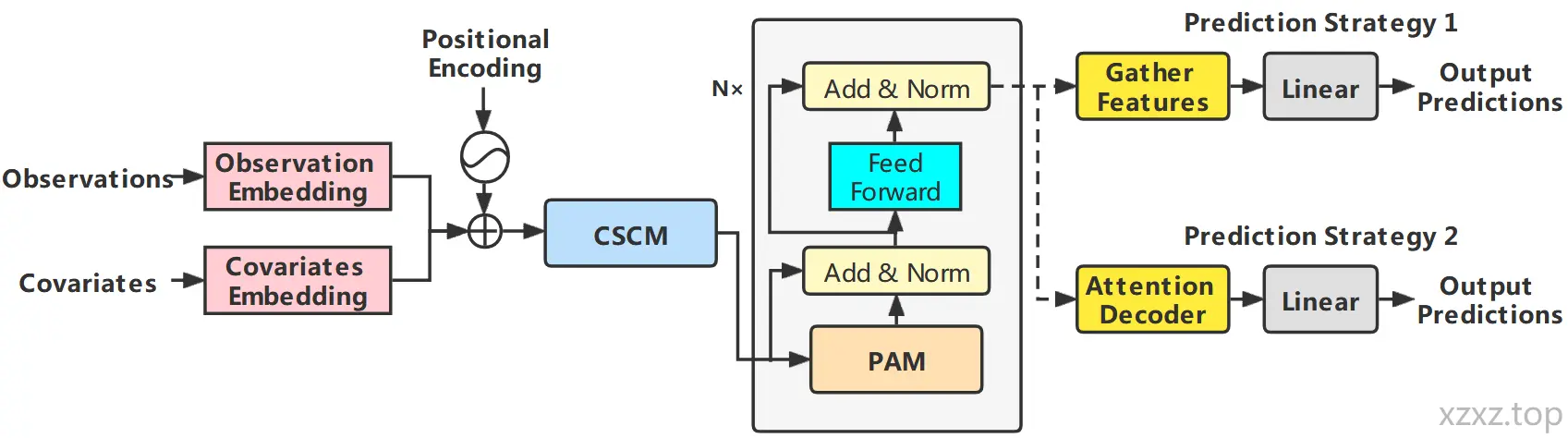
图 2：Pyraformer 的架构示意图：CSCM 对不同尺度上的嵌入序列进行汇总，构建出一个多分辨率树结构；随后，PAM 被用于在节点之间高效地交换信息。

方法

时间序列预测问题可以被形式化为：在已知前 $L$ 个观测值 $z_{t-L+1:t}$ 和相关协变量 $x_{t-L+1:t+M}$（例如一天中的小时）后，预测未来 $M$ 个时间步的值 $z_{t+1:t+M}$。

为实现这一目标，本文提出了 Pyraformer，其整体架构如图 2 所示。如图所示，我们首先对观测数据、协变量以及位置编码分别进行嵌入，并将它们相加，这一做法与 Informer 相似。

接下来，我们使用粗尺度构造模块（coarser-scale construction module, CSCM） 构建一个多分辨率的 $C$-叉树，在该结构中，粗尺度的节点汇总了相应细尺度上 $C$ 个节点的信息。

为了进一步捕捉不同范围的时间依赖关系，我们引入了金字塔注意力模块（pyramidal attention module, PAM），通过在金字塔图中基于注意力的消息传递机制实现信息交互。

最后，根据下游任务的不同，我们采用不同的网络结构来输出最终预测结果。在后续部分，我们将详细介绍该模型的每个组成部分。为了便于理解，本文所有符号的含义在表 4 中进行了汇总。

金字塔注意力模块（PAM）

我们从介绍 PAM 开始，因为它是 Pyraformer 的核心模块。如图 1(d) 所示，我们使用一个金字塔图结构来表示观测时间序列中的时间依赖关系，并以多分辨率方式进行建模。这种多尺度结构已被证明是计算机视觉和统计信号处理中一种高效且有效的长距离交互建模工具。

我们可以将金字塔图结构分解为两个部分：跨尺度连接和同尺度连接。其中，跨尺度连接构成一棵 $C$-叉树，在这棵树中，每个父节点拥有 $C$ 个子节点。例如，当我们将图中最细的尺度与原始时间序列中的小时观测点对应时，更粗尺度的节点可以表示天、周甚至月的特征。因此，金字塔图为原始时间序列提供了一种多分辨率表示。

此外，在更粗的尺度中，只需通过同尺度连接将相邻节点连接起来，就可以更容易地捕捉到长距离依赖关系（如月度周期）。换句话说，粗尺度对于建模长程相关性至关重要，这种图结构在图上的表现远比在单一细粒度尺度模型中直接连接所有节点更加简洁有效。

事实上，原始的单尺度 Transformer（见图 1(a)）采用的是完全连接图，即将最细尺度中所有节点两两相连，以建模长程依赖，这导致模型的时间和空间复杂度达到 $\mathcal{O}(L^2)$，在计算上非常繁重。与此形成鲜明对比的是，Pyraformer 所采用的金字塔图结构将计算成本降至 $\mathcal{O}(L)$，同时不会增加信号传递路径的最大长度的阶数。

在深入介绍 PAM 之前，我们先回顾原始的注意力机制。设 $X$ 和 $Y$ 分别表示一个单独注意力头的输入与输出。需要注意的是，可以引入多个注意力头以从不同视角捕捉时间模式。$X$ 首先被线性变换为三个不同的矩阵：查询矩阵 $Q = XW_Q$、键矩阵 $K = XW_K$、值矩阵 $V = XW_V$，其中 $W_Q, W_K, W_V \in \mathbb{R}^{L \times D_K}$。

对于 $Q$ 中的第 $i$ 行 $q_i$，它可以关注 $K$ 中的任意一行（即任意 key）。换句话说，其对应的输出 $y_i$ 可表示为：

$$y_i = \sum_{\ell=1}^{L} \frac{ \exp\left(q_i k_\ell^T / \sqrt{D_K} \right) v_\ell}{\sum_{\ell=1}^{L} \exp\left(q_i k_\ell^T / \sqrt{D_K} \right)}$$

其中，$k_\ell^T$ 表示 $K$ 中第 $\ell$ 行的转置。

我们特别强调，注意力机制的时间和空间复杂度主要由需要计算和存储的 query-key 点积（Q-K 对）的数量决定。换句话说，这个数量等价于图中边的数量（参考图 1(a)）。

由于在全量注意力机制中会计算并存储所有的 Q-K 对，因此其最终的时间和空间复杂度为 $\mathcal{O}(L^2)$。

与上述的全量注意力机制不同，在 PAM 中，每个节点只关注一组有限的 key，这些 key 对应于图 1(d) 中的金字塔图结构。具体地，设 $n_\ell^{(s)}$ 表示第 $s$ 层中的第 $\ell$ 个节点，其中 $s = 1, \cdots, S$ 表示从底层到顶层的尺度。

一般来说，图中每个节点可以关注其在三个尺度下的邻居节点集合 $\mathcal{N}_\ell^{(s)}$：包括同尺度的 $A$ 个邻居（包括自己，记作 $\mathcal{A}_\ell^{(s)}$）、在 $C$-叉树中的 $C$ 个子节点（记作 $\mathcal{C}_\ell^{(s)}$）、以及其在树中的父节点（记作 $\mathcal{P}_\ell^{(s)}$）。因此，有：

$$\begin{cases} \mathcal{N}_\ell^{(s)} = \mathcal{A}_\ell^{(s)} \cup \mathcal{C}_\ell^{(s)} \cup \mathcal{P}_\ell^{(s)} \\ \mathcal{A}_\ell^{(s)} = \left\{ n_j^{(s)} : |j - \ell| \leq \frac{A - 1}{2},\ 1 \leq j \leq \frac{L}{C^{s-1}} \right\} \\ \mathcal{C}_\ell^{(s)} = \left\{ n_j^{(s-1)} : (\ell - 1)C < j \leq \ell C \right\} \quad \text{若 } s \geq 2\text{，否则为空集} \\ \mathcal{P}_\ell^{(s)} = \left\{ n_j^{(s+1)} : j = \left\lceil \frac{\ell}{C} \right\rceil \right\} \quad \text{若 } s \leq S - 1\text{，否则为空集} \end{cases} \tag{2}$$

这个公式含义就是：我们希望每个节点只关注自己“附近”的节点，来减少计算量。这些“附近的节点”来自三种连接关系。 公式邻居集合符号解释：

1. $\mathcal{N}_\ell^{(s)}$：表示节点 $n_\ell^{(s)}$ 所能关注的全部邻居集合。
2. $\mathcal{A}_\ell^{(s)}$：同尺度邻居
   • 包含当前节点所在层（第 $s$ 层）中、距离不超过 $\frac{A - 1}{2}$ 的左右邻居节点（也包括自己）。
   • 上限是该层的节点总数，即 $\frac{L}{C^{s-1}}$。
3. $\mathcal{C}_\ell^{(s)}$：子节点（向下）
   • 当前节点在第 $s$ 层，如果 $s \geq 2$，它有 $C$ 个来自第 $s-1$ 层的子节点，索引范围是 $(\ell - 1)C < j \leq \ell C$。
4. $\mathcal{P}_\ell^{(s)}$：父节点（向上）
   • 当前节点在第 $s$ 层，如果 $s \leq S - 1$，它在第 $s+1$ 层有一个父节点，其索引为 $\left\lceil \frac{\ell}{C} \right\rceil$。

如果我们以一个 3 层结构为例，某个节点会看：

• 同层的左右邻居节点（局部窗口）
• 它对应的子节点（下一级更细分辨率）
• 它的父节点（上一级更粗分辨率）

这样的结构能捕捉多尺度的时序依赖，又保持高效。

由此，节点 $n_\ell^{(s)}$ 的注意力可以简化为仅对其邻居集合中的节点做加权平均：

$$y_i = \sum_{\ell \in \mathcal{N}_\ell^{(s)}} \frac{ \exp(q_i k_\ell^T / \sqrt{d_K}) v_\ell }{ \sum_{\ell \in \mathcal{N}_\ell^{(s)}} \exp(q_i k_\ell^T / \sqrt{d_K}) } \tag{3}$$

其中：

• $q_i$：第 $i$ 个节点的查询向量
• $k_\ell$：邻居节点的键向量
• $v_\ell$：邻居节点的值向量
• $\mathcal{N}_\ell^{(s)}$：节点能关注的邻居集合
• $d_K$：键向量维度，用于缩放稳定性

我们进一步用 $N$ 表示注意力层的数量。为了简化分析，假设 $L$ 能被 $C^{S-1}$ 整除。在此设定下，我们可以得到一个引理（证明见附录 B，相关符号见表 4）。

也就是一旦确定了每个节点所关注的邻居 $\mathcal{N}_\ell^{(s)}$，我们就只对这些邻居应用注意力，而不是对整个序列做注意力计算。

在我们的实验中，我们固定了 $S$ 和 $N$，并将 $A$ 设置为 3 或 5，不随序列长度 $L$ 的变化而改变。因此，所提出的 PAM 能够在实现 $\mathcal{O}(L)$ 的复杂度的同时，保持最大路径长度为 $\mathcal{O}(1)$。需要注意的是，在 PAM 中，一个节点最多只会关注 $A + C + 1$ 个节点。不幸的是，这种稀疏注意力机制在现有的深度学习库（如 PyTorch 和 TensorFlow）中并不被原生支持。

一个简单但幼稚的实现方式是：首先计算所有 Q-K 对的点积，即 $q_i k_\ell^T$（$\ell = 1, \cdots, L$），然后将不属于邻接集合 $\mathcal{N}_\ell^{(s)}$ 的项进行掩码（mask）。然而，这种实现方式的时间和空间复杂度依然是 $\mathcal{O}(L^2)$。

为了解决这一问题，我们使用 TVM 框架为 PAM 构建了一个专门定制的 CUDA 内核，在实际运行中有效地减少了计算时间和内存开销，从而使得所提出的模型更适用于长时间序列的建模。通常来说，更长的历史输入有助于提高预测准确率，因为提供了更多信息，尤其是在建模长距离依赖关系时这一点尤为重要。

引理 1（Lemma 1）

给定参数 $A$、$C$、$L$、$N$、$S$，若满足以下条件：

$$\frac{L}{C^{S-1}} - 1 \leq \frac{(A - 1)N}{2} \tag{4}$$

则在经过 $N$ 层堆叠的注意力之后，金字塔结构最顶层的节点将拥有全局感受野。此外，当尺度数量 $S$ 固定时，以下两个命题总结了 Pyraformer 所提出的金字塔注意力机制的时间与空间复杂度，以及其信号传递路径长度的阶数（相关证明见附录 C 和 D）：

命题 1（Proposition 1）

对于给定的 $A$ 和 $L$，金字塔注意力机制的时间与空间复杂度为 $\mathcal{O}(AL)$。 当 $A$ 相对于 $L$ 为常数时，复杂度可简化为 $\mathcal{O}(L)$。

命题 2（Proposition 2）

设图中两个节点之间的信号传递路径为连接它们的最短路径。则金字塔图中任意两节点之间的最大信号传递路径长度为：

$$\mathcal{O}\left(S + \frac{L}{C^{S-1} A} \right)$$

对于给定的 $A$、$C$、$L$、$S$，若 $A$ 和 $S$ 为常数，且 $C$ 满足如下条件：

$$\sqrt[S-1]{L} \geq C \geq \sqrt[S-1]{\frac{L}{(A - 1)N/2 + 1}} \tag{5}$$

那么最大路径长度为 $\mathcal{O}(1)$，即路径长度与时间序列长度 $L$ 无关。

粗尺度构造模块（CSCM）

CSCM 的目标是初始化金字塔图中粗尺度的节点，以便后续的 PAM 能够在这些节点之间高效地交换信息。具体而言，粗尺度节点是通过对其对应的子节点（记作 $C_\ell^{(s)}$）进行卷积操作，从底向上逐层构建的。

如图 3 所示，我们在时间维度上对嵌入序列连续应用多个卷积层，每层卷积核大小为 $C$，步长也为 $C$，在第 $s$ 层得到长度为 $L / C^s$ 的序列。不同尺度下的输出共同构成一棵 $C$-叉树。

我们将这些从细到粗的序列拼接在一起，作为 PAM 的输入。为减少参数量与计算量，我们在进入堆叠卷积层之前，通过一个全连接层将每个节点的维度先压缩，在所有卷积操作完成后再将其还原。这种瓶颈结构（bottleneck structure） 在显著降低模块参数数量的同时，也有助于防止过拟合。

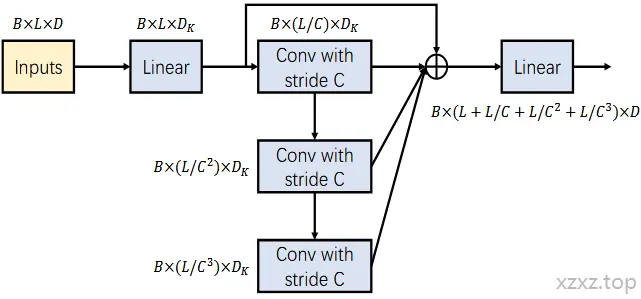
图 3：粗尺度构造模块示意图。$B$ 表示批大小，$D$ 表示节点的特征维度。

预测模块（Prediction Module）

对于单步预测，我们在历史序列 $z_{t-L+1:t}$ 的末尾添加一个终止标记（即设置 $z_{t+1} = 0$），然后输入嵌入层。经过 PAM 编码后，我们提取金字塔图中各尺度上最后一个节点的特征，将其拼接后输入一个全连接层用于预测。

对于多步预测，我们提出了两种预测模块：

• 第一种与单步预测模块相同，但将各尺度上最后一个节点的特征一次性映射为 $M$ 个未来时间步的输出，即批量预测。
• 第二种则采用一个包含两个全注意力层（full-attention）的解码器。

具体地，类似于原始 Transformer，我们将未来 $M$ 个时间步的观测值设为 0，并与历史观测一样进行嵌入，记其观测嵌入、协变量嵌入和位置嵌入之和为预测 token $F_p$。

• 第一个注意力层以 $F_p$ 为 query，PAM 编码器的输出（即所有节点）$F_e$ 为 key 和 value，输出为 $F_{d1}$。
• 第二个注意力层以 $F_{d1}$ 为 query，以 $F_{d1} \cup F_e$ 为 key 和 value。
• 编码器输出 $F_e$ 被直接送入两个注意力层，因为历史信息对长距离预测至关重要。

最终预测结果通过一个跨通道维度的全连接层生成。需要强调的是，我们一次性输出所有未来时间步的预测值，以避免传统 Transformer 自回归解码器中的误差累积问题。

符号	维度	含义
$L$	常量	历史序列的长度
$G$	常量	ETC 中全局 token 的数量
$M$	常量	需要预测的未来序列长度
$B$	常量	批大小（batch size）
$D$	常量	每个节点的特征维度
$D_K$	常量	key 的维度
$\mathbf{X}$	$B \times L \times D$	单个注意力头的输入
$\mathbf{Y}$	$B \times L \times D$	单个注意力头的输出
$\mathbf{Q}$	$B \times L \times D_K$	查询向量（Query）
$\mathbf{K}$	$B \times L \times D_K$	键向量（Key）
$\mathbf{V}$	$B \times L \times D_K$	值向量（Value）
$\mathbf{W}_Q$	$D \times D_K$	查询的权重矩阵
$\mathbf{W}_K$	$D \times D_K$	键的权重矩阵
$\mathbf{W}_V$	$D \times D_K$	值的权重矩阵
$S$	常量	金字塔结构中的尺度数量
$A$	常量	同一尺度中，一个节点可关注的相邻节点数
$C$	常量	每个粗尺度节点所汇总的细尺度节点数量
$N$	常量	注意力层的层数
$n_\ell^{(s)}$	$D$	第 $s$ 层中的第 $\ell$ 个节点
$\mathcal{N}_\ell^{(s)}$	$\text{len}(\mathcal{N}_\ell^{(s)}) \times D$	节点 $n_\ell^{(s)}$ 的邻接节点集合
$\mathcal{A}_\ell^{(s)}$	$\text{len}(\mathcal{A}_\ell^{(s)}) \times D$	与 $n_\ell^{(s)}$ 同尺度相邻的 $A$ 个节点
$\mathcal{C}_\ell^{(s)}$	$\text{len}(\mathcal{C}_\ell^{(s)}) \times D$	$n_\ell^{(s)}$ 对应的子节点
$\mathcal{P}_\ell^{(s)}$	$\text{len}(\mathcal{P}_\ell^{(s)}) \times D$	$n_\ell^{(s)}$ 对应的父节点
$\mathbf{F}_p$	$B \times M \times D$	预测 token（未来 M 步的嵌入）
$\mathbf{F}_e$	$B \times L_{\text{tot}} \times D$	编码器的输出，$L_{\text{tot}}$ 为输出序列总长度
$\mathbf{F}_{d1}$	$B \times M \times D$	解码器第一层的输出
$H$	常量	注意力头的数量
$D_F$	常量	前馈层的最大维度（hidden size）

表4：符号的含义。