iTransformer

论文名称：iTransformer: Inverted Transformers Are Effective for Time Series Forecasting
论文地址：https://arxiv.org/abs/2310.06625 (opens new window)
引用量（截止到2025.07.08）：1244
Venue：ICLR 2024

一句话总结这篇论文

不用与其他方法将相同时间的不同变量作为一个token，这篇论文将的不同时间的相同变量的序列作为token。直观展示间下文图 2.

摘要

近期线性预测模型的兴起，质疑了持续对基于Transformer预测器架构修改的热情。这些预测器利用Transformer对时间序列中时间token之间的全局依赖关系进行建模，每个token由同一时间点的多个变量组成。然而，当预测器面对更长的历史窗口时，Transformer容易出现性能下降与计算开销激增的问题。此外，每个时间token的嵌入融合了多个可能存在延迟的事件和物理测量方式各异的变量，难以学习以变量为中心的表示，从而导致注意力图缺乏意义。在本研究中，我们重新审视了Transformer组件的职责，在不修改基础组件的前提下重新设计其架构。我们提出了iTransformer，它仅通过在倒置维度上应用注意力机制和前馈网络来实现。具体而言，我们将单个变量的时间序列嵌入为“变量token”，利用注意力机制捕捉变量间的相关性；同时，对每个变量token应用前馈网络以学习非线性表示。iTransformer在多个具有挑战性的真实数据集上取得了当前最优性能（state-of-the-art），进一步提升了Transformer家族在性能、跨变量泛化能力及对任意历史窗口的适应性方面的表现，使其成为时间序列预测中理想的基础架构选择。代码开源地址：https://github.com/thuml/iTransformer。 (opens new window)

引言

Transformer 在自然语言处理和计算机视觉领域取得了巨大的成功，逐渐成为遵循扩展规律的基础模型。受其在多个领域广泛成功的启发，Transformer 由于其在刻画成对依赖关系和提取序列多层次表示方面的强大能力，正逐渐被应用于时间序列预测。

然而，研究者们近年来开始质疑基于 Transformer 的预测模型的有效性。这类模型通常将同一时间点的多个变量嵌入为不可区分的通道，并在这些时间 token 上应用注意力机制以捕捉时间依赖关系。鉴于时间点之间主要是数值而非语义关联，研究发现，一些简单的线性层模型（其原理可追溯至传统统计预测方法），在性能和效率上都超越了复杂的 Transformer 模型。与此同时，变量间独立性以及变量之间互信息的利用也越来越受到关注，许多研究开始显式建模多变量之间的相关性以实现更准确的预测。但要实现这一目标，几乎不可能不对原始的 Transformer 架构进行根本性调整。

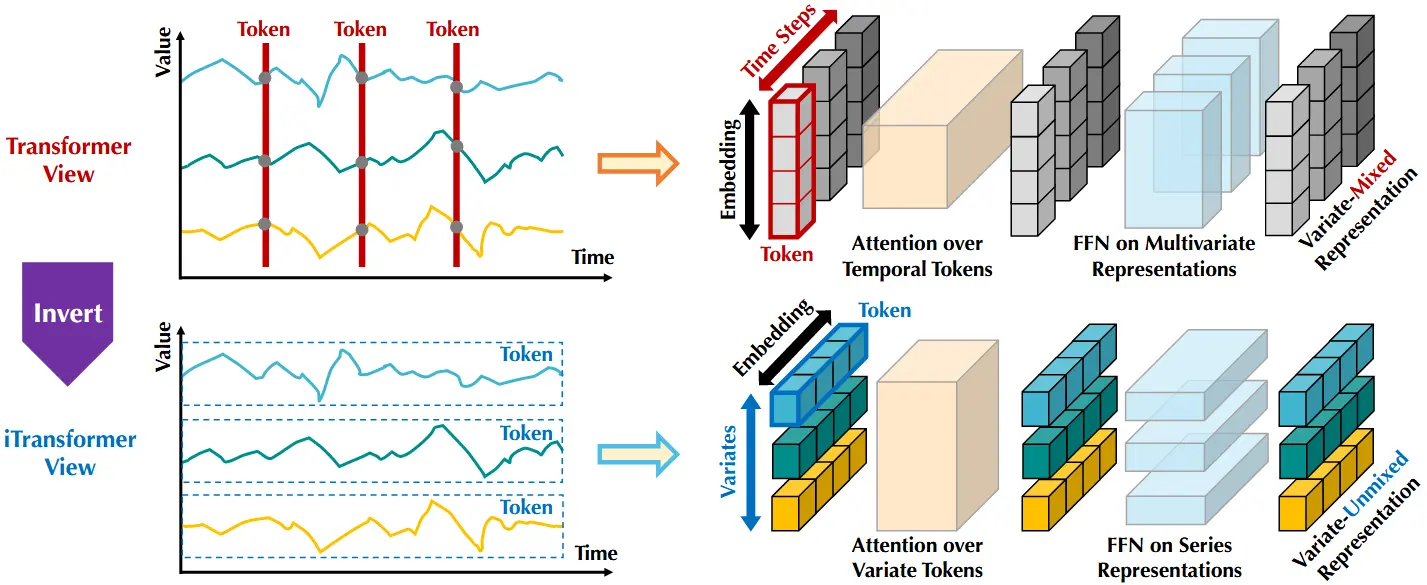
图 2：比较了 vanilla Transformer（上）与本文提出的 iTransformer（下）之间的差异。vanilla Transformer 将每个时间步的多变量表示作为一个时间 token进行嵌入。而 iTransformer 则是将每个变量的完整序列分别嵌入为变量 token，从而使注意力机制能够建模变量之间的相关性，前馈网络则用于提取序列的表示特征。

鉴于人们对基于 Transformer 的时间序列预测模型的争议，我们重新思考了为何 Transformer 在时间序列预测中的表现甚至不如简单的线性模型，而在其他领域却表现出色。我们注意到，现有的 Transformer 架构并不适用于多变量时间序列预测。如图2上部所示，同一时间步的多个数据点，本质上代表了物理意义完全不同、测量方式也各异的变量，却被嵌入为一个统一的 token，从而抹除了变量之间的相关性。而且，由单个时间步构成的 token 由于感受野过小，以及时间点间事件未对齐的问题，往往难以提供有用的信息。

此外，尽管序列变化高度依赖于时间顺序，Transformer 却在时间维度上错误地采用了置换不变的注意力机制。结果，Transformer 难以捕捉关键的时间序列表示和变量间的相关性，限制了其在多样化时间序列数据上的建模能力与泛化能力。

考虑到将多个变量嵌入为一个时间 token 所带来的潜在风险，我们提出了一个倒置视角：将每个变量的完整时间序列独立地嵌入为一个“变量 token”。这可以被视为一种极端的 Patch 化操作，用以扩大局部感受野。通过这种倒置方式，每个 token 能够聚合整个变量序列的全局表示，更加以变量为中心，从而可以更好地利用注意力机制来刻画变量间的相关性。与此同时，前馈网络则被用于每个变量 token 的时间建模，能够有效地从任意历史长度中学习出具有泛化能力的表示，并用于预测未来的序列。

基于上述动机，我们认为，Transformer 并不是在时间序列预测中无效，而是被错误地使用了。因此，在本文中，我们重新审视了 Transformer 的结构，提出了 iTransformer，作为时间序列预测的基础骨干模型。

在技术实现上，我们将每个时间序列嵌入为变量 token，通过自注意力机制建模变量间的相关性，并通过前馈网络学习时间序列的表示。在实验上，iTransformer 在图1所示的多个真实预测基准数据集上取得了当前最优性能（state-of-the-art），并成功解决了 Transformer 在时间序列任务中的多个痛点。

我们的主要贡献体现在以下三个方面：

• 我们反思了 Transformer 架构，指出其原生组件在多变量时间序列中的潜在能力尚未被充分挖掘。

• 我们提出了 iTransformer，将每个独立时间序列视为一个 token，利用自注意力机制捕捉变量间的相关性，同时结合层归一化与前馈网络模块，学习更具全局性的时间序列表示。

• 在实验中，iTransformer 在多个真实数据集上取得全面领先的表现，我们还系统分析了倒置结构的组件与架构选择，揭示了未来 Transformer 时间序列模型改进的潜在方向。

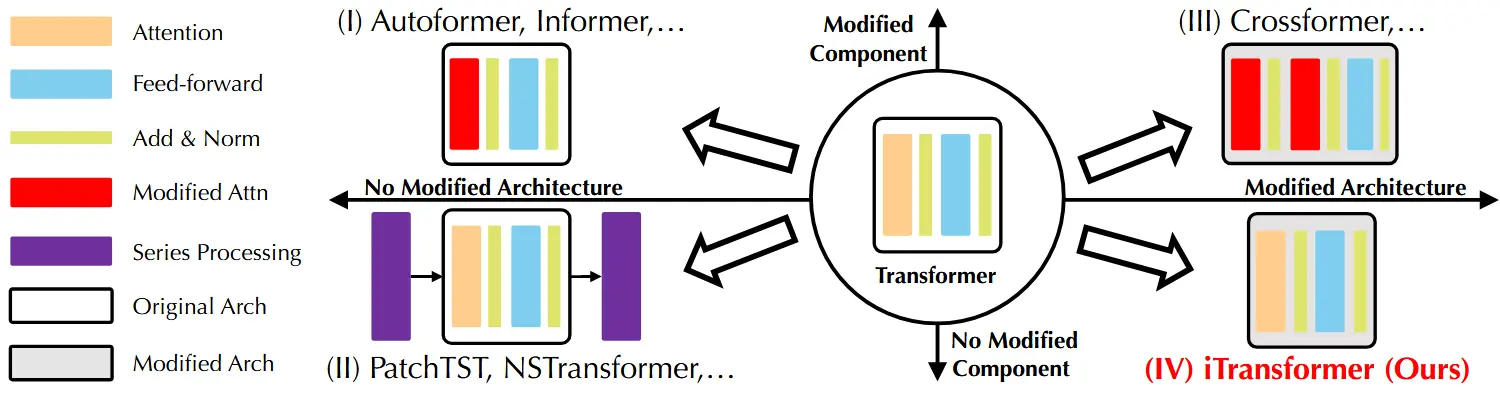
图 3：基于 Transformer 的预测模型按照组件修改与架构修改进行分类。

相关工作

随着自然语言处理和计算机视觉领域的持续突破，许多精心设计的 Transformer 变体被提出，用以应对广泛存在的时间序列预测任务。超越了传统的 TCN（时序卷积网络）和基于 RNN 的预测方法，Transformer 展现出强大的序列建模能力和良好的可扩展性，促使大量研究开始热衷于将其架构加以改造，以适配时间序列任务。

通过系统回顾现有的基于 Transformer 的时间序列预测模型，我们将这些模型的改进方式按照是否修改组件与架构，划分为以下四类（如图3所示）：

• 第一类是目前最常见的做法，主要在组件层面进行调整，尤其集中在注意力机制的改造，以更好地建模时间依赖性并优化长序列下的计算复杂度。

• 第二类试图更加充分地利用 Transformer 的潜力，重点在于针对时间序列本身的特性进行处理，例如序列平稳化（Stationarization）、通道独立建模（Channel Independence）以及打补丁（Patching）等方法，这些通常能带来稳定的性能提升。

• 第三类则在组件与架构两个层面同时进行重构。典型方法通过改进的注意力机制与架构，明确捕捉时间维度与变量维度之间的交叉依赖关系。

• iTransformer 属于第四类：不同于以往所有工作，它没有修改任何原生的 Transformer 组件，而是直接在倒置的维度上使用这些组件，并对架构进行了重构。我们认为，Transformer 的各个组件本身已经在其他任务中被充分验证，问题在于其在时间序列任务中被错误地使用了。

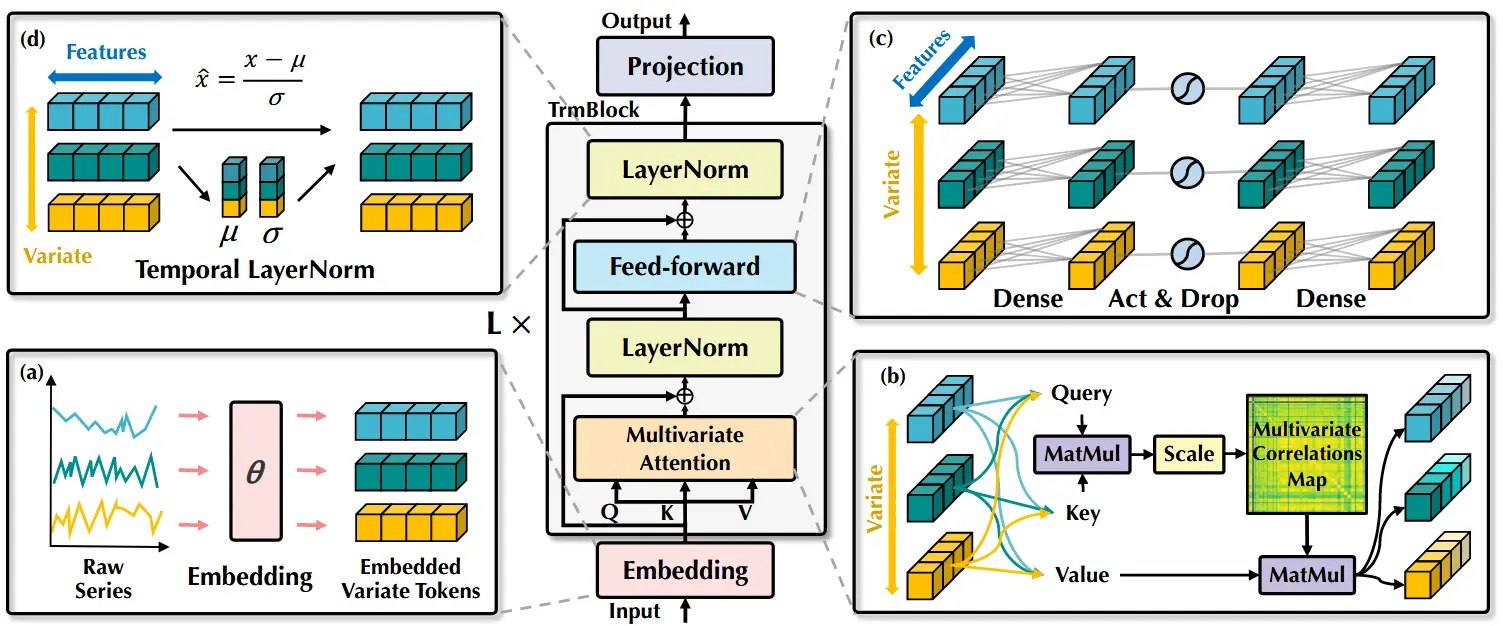
图 4：iTransformer 的整体结构，与 Transformer 的编码器具有相同的模块化排列。(a) 不同变量的原始时间序列被分别嵌入为 token；(b) 对嵌入后的变量 token 应用自注意力机制，以增强可解释性并揭示多变量间的相关性；(c) 每个 token 的序列表示由共享的前馈网络提取；(d) 采用层归一化以减少不同变量之间的差异。

iTransformer

在多变量时间序列预测中，给定历史观测值 $\mathbf{X} = \{\mathbf{x}_1, \ldots, \mathbf{x}_T\} \in \mathbb{R}^{T \times N}$，其中 $T$ 表示时间步数，$N$ 表示变量数，我们的目标是预测未来 $S$ 个时间步的序列 $\mathbf{Y} = \{\mathbf{x}_{T+1}, \ldots, \mathbf{x}_{T+S}\} \in \mathbb{R}^{S \times N}$。

为简便起见，我们记 $\mathbf{X}_{t,:}$ 为第 $t$ 个时间步上所有变量的观测值，$\mathbf{X}_{:,n}$ 为第 $n$ 个变量在整个时间序列上的观测值。（这里注意区分下标 $t$，$:$，$n$ 的位置）

值得注意的是，$\mathbf{X}_{t,:}$ 中的变量在真实场景中不一定代表同一个事件，这是由于数据中变量间存在系统性的时间滞后。此外，$\mathbf{X}_{t,:}$ 的各个元素在物理测量维度和统计分布上可能具有差异，而 $\mathbf{X}_{:,n}$ 通常共享这些特性。

结构概览

我们提出的 iTransformer（如图 4 所示）采用了 Transformer 的仅编码器（encoder-only）架构，包括嵌入（embedding）、投影（projection）以及 Transformer 块。

将整个序列作为 token 进行嵌入

多数基于 Transformer 的预测模型通常将同一时间点的多个变量作为（时间）token，并遵循生成式的预测任务建模方式。然而，我们发现，这种在数值模态上的建模方法对于学习注意力图的指导性较弱，这一观点也得到了对“Patch”方法日益增长的应用所支持，这类方法拓宽了感受野。

与此同时，线性预测模型的成功进一步质疑了使用复杂的编码器-解码器结构生成 token 的必要性。因此，我们提出的仅编码器结构的 iTransformer 更加专注于表示学习和多变量序列之间的自适应关联建模。每一条由复杂动态过程驱动的时间序列，首先被嵌入为 token，以描述该变量的特征，随后通过自注意力机制捕捉变量间的相互关系，并分别通过前馈网络提取各变量的序列表示。

值得注意的是，生成预测序列的任务本质上是由线性层完成的，这在以往的研究中已被证明是有效的，我们将在下一节中对此进行详细分析。

根据上述思路，在 iTransformer 中，预测某一特定变量 $\hat{\mathbf{Y}}_{:,n}$ 的未来序列（基于其回溯序列 $\mathbf{X}_{:,n}$）的过程可被简洁地表示如下：

$$\begin{aligned} \mathbf{h}^0_n &= \text{Embedding}(\mathbf{X}_{:,n}), \\ \mathbf{H}^{l+1} &= \text{TrmBlock}(\mathbf{H}^l), \quad l = 0, \ldots, L-1, \\ \hat{\mathbf{Y}}_{:,n} &= \text{Projection}(\mathbf{h}^L_n), \end{aligned}$$

其中，$\mathbf{H} = \{\mathbf{h}_1, \ldots, \mathbf{h}_N\} \in \mathbb{R}^{N \times D}$ 表示维度为 $D$ 的 $N$ 个嵌入 token，右上角的上标表示网络层编号。函数 Embedding: $\mathbb{R}^T \mapsto \mathbb{R}^D$ 和 Projection: $\mathbb{R}^D \mapsto \mathbb{R}^S$ 均由多层感知机（MLP） 实现。

获得的变量 token 之间通过自注意力机制进行交互，并在每一层 TrmBlock 中由共享的前馈网络独立处理。值得强调的是，由于序列的顺序信息已隐式地编码在前馈网络的神经元排列中，因此在此结构中不再需要 vanilla Transformer 中的位置编码（position embedding）。

iTransformers

该架构本质上对 Transformer 的变体没有额外的特定要求，只需注意力机制能够用于建模多变量间的相关性。因此，许多高效的注意力机制（例如 Li et al., 2021；Wu et al., 2022；Dao et al., 2022）都可以作为插件使用，在变量数量较多时有效降低计算复杂度。

此外，借助注意力机制的输入灵活性，token 的数量在训练和推理阶段可以不同，模型也允许在任意数量的变量上进行训练。该倒置架构下的 Transformer，被称为 iTransformers，在第 4.2 节的实验中得到了广泛评估，并在时间序列预测任务中展现出明显优势。

倒置 Transformer 组件

我们组织了一个包含 $L$ 层的堆叠结构，每层由层归一化（layer normalization）、前馈网络（feed-forward network） 和自注意力模块（self-attention module） 组成。但在倒置维度下，这些模块的功能被重新设计和思考。

层归一化（Layer normalization）

层归一化最初是为了提高深度网络的收敛速度和训练稳定性。在传统的 Transformer 预测模型中，该模块通常对同一时间步的多变量表示进行归一化，逐步融合各变量的信息。

然而，当同一时间步的各变量并不代表同一真实事件时，这种做法会引入非因果或延迟过程之间的噪声干扰。在我们的倒置版本中，归一化操作被应用于单个变量的序列表示，如公式（2）所示。这种做法已经被证明在处理非平稳性问题中是有效的。

此外，由于所有序列（即变量 token）都被归一化为高斯分布，因此由不同测量尺度带来的差异也能被减弱。相比之下，在传统架构中，不同时间步的 token 被归一化，反而可能导致时间序列过度平滑。

$$\text{LayerNorm}(\mathbf{H}) = \left\{ \frac{\mathbf{h}_n - \text{Mean}(\mathbf{h}_n)}{\sqrt{\text{Var}(\mathbf{h}_n)}} \;\middle|\; n = 1, \ldots, N \right\} \quad \text{(2)}$$

前馈网络（Feed-forward network）

Transformer 使用前馈网络（FFN）作为编码 token 表示的基本构件，并对每个 token 应用相同的结构。在原始 Transformer 中，将多个变量在同一时间步组合为 token 往往存在位置错乱，且信息过于局部，难以提供有效的预测线索。

在倒置版本中，FFN 被用于每个变量 token 的整个序列表示。根据通用近似定理，它们能够提取出复杂的时间序列特征。通过堆叠多层倒置结构，这些网络能够编码观测到的时间序列，并通过密集的非线性连接解码出预测表示，这种方式在基于 MLP 的最新模型中已经被证明是非常有效的。

更有趣的是，对独立时间序列应用相同的线性操作，正是近期线性预测模型和 Channel Independence 方法的组合思路。这为我们理解序列表示学习提供了启发。最新研究表明，MLP 所提取的时间特征具有可迁移性，能够在不同时间序列之间共享。

我们给出一个合理解释：MLP 的神经元被训练来刻画任意时间序列的内在属性，如振幅、周期性，甚至频谱成分（可以视作“神经元即滤波器”）。因此，相比于作用在时间点上的注意力机制，前馈网络在预测表示学习中更具优势。实验中我们也验证了这一职责分工的好处（详见 4.3 节）：例如，在使用更长回溯窗口时能带来性能提升，同时也具备对未见变量的泛化能力。

自注意力机制（Self-attention）

尽管传统预测器通常利用注意力机制来建模时间依赖关系，但在倒置模型中，每个变量的完整序列被视为一个独立的过程。具体来说，对于每个时间序列，其提取的表示为 $\mathbf{H} = \{\mathbf{h}_0, \ldots, \mathbf{h}_N\} \in \mathbb{R}^{N \times D}$，自注意力模块通过线性映射生成查询、键和值，分别为 $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d_k}$，其中 $d_k$ 是投影后的维度。

设定 $\mathbf{q}_i, \mathbf{k}_j \in \mathbb{R}^{d_k}$ 为两个变量 token 的查询和键，我们可以得到 pre-Softmax 的打分项：

$$A_{i,j} = \left( \frac{\mathbf{QK}^\top}{\sqrt{d_k}} \right)_{i,j} \propto \mathbf{q}_i^\top \mathbf{k}_j$$

由于每个 token 在特征维度上已被归一化，因此这些打分项在一定程度上反映了变量间的相关性。整个打分矩阵 $\mathbf{A} \in \mathbb{R}^{N \times N}$ 则表示所有变量之间的互相关系。

因此，高度相关的变量将被赋予更大的权重，以参与下一步与 $\mathbf{V}$ 的表示交互。基于这种直觉，所提出的注意力机制被认为更自然且更具可解释性，适用于多变量时间序列预测。相关注意力图的可视化分析见 4.3 节与附录 E.1。