1 Autoformer

论文名称：Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting
论文地址：https://proceedings.neurips.cc/paper/2021/hash/bcc0d400288793e8bdcd7c19a8ac0c2b-Abstract.html (opens new window)
引用量（截止到2025.07.08）：3292
Venue：NeurIPS 2021
代码开源地址：https://github.com/thuml/Autoformer (opens new window)
Star 数量：2200+

2 一句话总结这篇论文

这篇论文主要提出了一个序列分解模块（其实就是一个Pooling操作，一个相减的操作，详细见5.4.1），自相关机制（其实就是使用傅里叶变换计算自相关的权重，来加权不同的周期特征，详细见5.8）。

3 摘要

延长预测时间在诸多实际应用中是关键需求，例如极端天气预警和长期能源消耗规划。本文研究时间序列的长期预测问题。已有的基于 Transformer 的模型采用多种自注意力机制来挖掘远程依赖关系，然而长期未来中的复杂时间模式阻碍了模型对可靠依赖的捕捉。此外，为了处理长序列的效率问题，Transformer 不得不采用稀疏版本的点对点自注意力机制，从而导致信息利用上的瓶颈。为突破 Transformer 的限制，我们设计了 Autoformer——一种新颖的分解架构，并引入了自相关机制。我们打破了将时间序列分解作为预处理的传统做法，将其重构为深度模型中的基本内部模块。这一设计赋予 Autoformer 渐进式地处理复杂时间序列的能力。此外，受随机过程理论启发，我们基于序列的周期性设计了自相关机制，在子序列层面上进行依赖关系的发现和表示的聚合。自相关机制在效率和准确性上都优于自注意力机制。在长期预测任务中，Autoformer 在六个基准数据集上实现了 38% 的相对精度提升，涵盖能源、交通、经济、气象和疾病五大实际应用场景。代码开源地址为：https://github.com/thuml/Autoformer。 (opens new window)

4 引言

时间序列预测被广泛应用于能源消耗、交通与经济规划、气象预报以及疾病传播预测等实际场景中。在这些现实应用中，一个紧迫的需求是将预测时间延长至更远的未来，这对于长期规划和预警具有重要意义。因此，本文聚焦于时间序列的长期预测问题，其特点是预测序列的长度较大。 近年来，深度预测模型取得了显著进展，特别是基于 Transformer 的方法。得益于自注意力机制（self-attention），Transformer 在建模序列数据的长期依赖关系方面具有巨大优势，从而使得构建更强大的大型模型成为可能。 然而，在长期预测设置下，这一任务依然极具挑战性：

1. 直接从长期时间序列中发现时间依赖关系并不可靠，因为这些依赖关系可能被复杂交织的时间模式所掩盖；
2. 传统的 Transformer 模型计算成本极高，因为其自注意力机制的复杂度随序列长度呈平方级增长（O(L²)），这使得其在长期预测中难以扩展。

尽管已有工作尝试通过将自注意力机制稀疏化来提升效率，并取得了显著的性能提升，但它们依然采用点对点的表示聚合方式。因此，在提高效率的过程中，这些模型会因为稀疏的点对点连接而牺牲信息利用率，导致时间序列长期预测面临信息瓶颈问题。

为了解释复杂的时间模式，我们引入了时间序列分析中的经典方法——序列分解。它可以帮助处理复杂的时间序列，并提取出更具可预测性的成分。然而，在预测任务中，分解通常仅作为历史序列的预处理使用，因为未来序列尚未知晓。这种常规用法限制了分解的能力，也忽略了被分解成分之间在未来可能存在的交互。

因此，我们尝试突破传统的预处理式分解方式，提出一种通用的深度模型架构，使其具备内在的、渐进式分解能力。分解有助于解开纠缠的时间模式，突出时间序列的固有属性。基于这一优势，我们进一步考虑利用序列的周期性，对自注意力机制中的点对点连接进行革新。

我们观察到，不同周期中相同相位位置的子序列通常呈现出相似的时间演化过程。因此，我们构造了一种基于周期性相似性的序列级连接机制，以替代原有的点对点注意力。基于上述动机，我们提出了Autoformer，用于替代传统 Transformer 进行长期时间序列预测。

Autoformer 仍保留了 Transformer 的残差结构和编码器-解码器框架，但我们将其重构为一个基于分解的预测架构。通过嵌入我们设计的序列分解模块，Autoformer 能够渐进式地从预测过程中的隐藏变量中提取长期趋势信息，并在预测过程中交替地分解与细化中间结果。

受随机过程理论启发，我们提出了 Auto-Correlation（自相关）机制，用于替代自注意力。该机制基于序列的周期性来发现子序列间的相似性，并从历史周期中聚合相似子序列。这一序列级机制的时间复杂度为 O(L log L)（L 为序列长度），并通过将点对点的表示聚合拓展为子序列级别，从而打破信息利用瓶颈。本文贡献如下：

• 为应对长期未来的复杂时间模式，我们提出了 Autoformer 分解架构，并设计了内部的分解模块，使深度预测模型具备内在的渐进式分解能力；
• 提出了 Auto-Correlation 机制，可在序列级别发现依赖关系并进行信息聚合，超越了传统的自注意力系列方法，在提升计算效率的同时增强了信息利用率；
• Autoformer 在六个长期预测基准任务上取得了38% 的相对性能提升，覆盖了五大真实应用场景：能源、交通、经济、气象与疾病。

5 相关工作

5.1 时间序列预测模型

由于时间序列预测在各类实际场景中具有极高的重要性，研究者已开发出多种有效模型。许多时间序列预测方法起步于经典统计工具。例如，ARIMA 通过差分将非平稳序列转化为平稳序列，以应对预测任务。滤波方法也被用于提取时间序列中的趋势或周期成分。

此外，循环神经网络（RNN） 被广泛用于建模时间序列中的时间依赖关系。例如，DeepAR 将自回归方法与 RNN 结合，用于建模未来序列的概率分布。LSTNet 融合卷积神经网络（CNN）和带跳跃连接的循环单元，用于同时捕捉短期与长期的时间模式。基于注意力机制的 RNN 引入了时间注意力机制，以增强对长距离依赖的建模能力。

同时，基于 时序卷积网络（Temporal Convolutional Network, TCN） 的方法也广泛应用于时间序列建模，这类方法使用因果卷积（causal convolution） 来保持时间顺序并建模因果关系。这些深度预测模型主要集中在时间关系建模，采用循环连接、时间注意力机制或因果卷积等技术手段。

近年来，基于自注意力机制（self-attention） 的 Transformer 模型在处理序列数据方面表现出强大能力，已广泛应用于自然语言处理、音频建模乃至计算机视觉任务中。然而，将自注意力机制应用于长期时间序列预测时，存在严重的计算效率问题。因为其在时间和空间上的复杂度为：$\mathcal{O}(L^2)$，其中 $L$ 为序列长度。

为了解决这一问题，研究者提出了若干改进方法以提升效率：

• LogTrans 在 Transformer 中引入局部卷积，并设计了 LogSparse 注意力机制，按照指数间隔选择关键时间点，将复杂度降低为：$\mathcal{O}(L(\log L)^2)$。
• Reformer 使用局部敏感哈希（LSH）注意力机制，将复杂度降低为：$\mathcal{O}(L \log L)$
• Informer 通过基于 KL 散度的 ProbSparse 注意力机制，也实现了：$\mathcal{O}(L \log L)$

需要指出的是，以上方法均基于原始 Transformer 架构，核心思想仍为点对点（point-wise）依赖建模与表示聚合，仅在连接稀疏性与效率方面做出改进。而在本文中，我们提出的 Auto-Correlation（自相关）机制 基于时间序列的固有周期性构建，可以实现序列级（series-wise）连接，在建模效率与信息利用方面都超越了传统的自注意力机制。

5.2 时间序列的分解方法

作为时间序列分析中的一种标准方法，时间序列分解将序列拆解为多个组成部分，每一部分代表一种更具可预测性的潜在模式。这种方法主要用于分析历史数据的变化趋势。在预测任务中，分解通常被用作对历史序列的预处理步骤，以便预测未来序列。例如，Prophet 使用趋势-季节性分解，N-BEATS 借助基函数展开，DeepGLO 则采用矩阵分解方法来提取不同成分。

然而，这种预处理方式存在局限性：

• 仅对历史序列进行静态分解；
• 忽略了未来序列中潜在模式之间的层级交互，尤其在长期预测中难以适应复杂结构。

本文提出了一种全新的渐进式分解视角。我们在 Autoformer 中将“序列分解”嵌入为深度模型的内部模块，使模型能够在整个预测过程中——包括对历史序列的处理和对中间预测结果的 refinement（细化）中，持续进行隐变量的动态分解，从而更好地刻画长期序列中的趋势与变化。

5.3 Autoformer

时间序列预测问题的目标是：给定长度为 $I$ 的历史序列，预测长度为 $O$ 的未来序列，记作 input-$I$-predict-$O$。其中，长期预测（long-term forecasting） 指的是预测更远期的未来，即 $O$ 较大。如前所述，长期预测面临两大核心挑战：

• 复杂时间模式的建模困难；
• 计算效率和信息利用的瓶颈。

为应对上述挑战，我们将序列分解机制引入为深度预测模型的内置模块，并据此提出Autoformer 架构，即一个基于分解的时间序列预测网络。此外，我们还设计了Auto-Correlation（自相关）机制，用于挖掘基于周期性的依赖关系，并从历史周期中聚合相似子序列，以提升模型对周期结构的感知能力和长期预测性能。

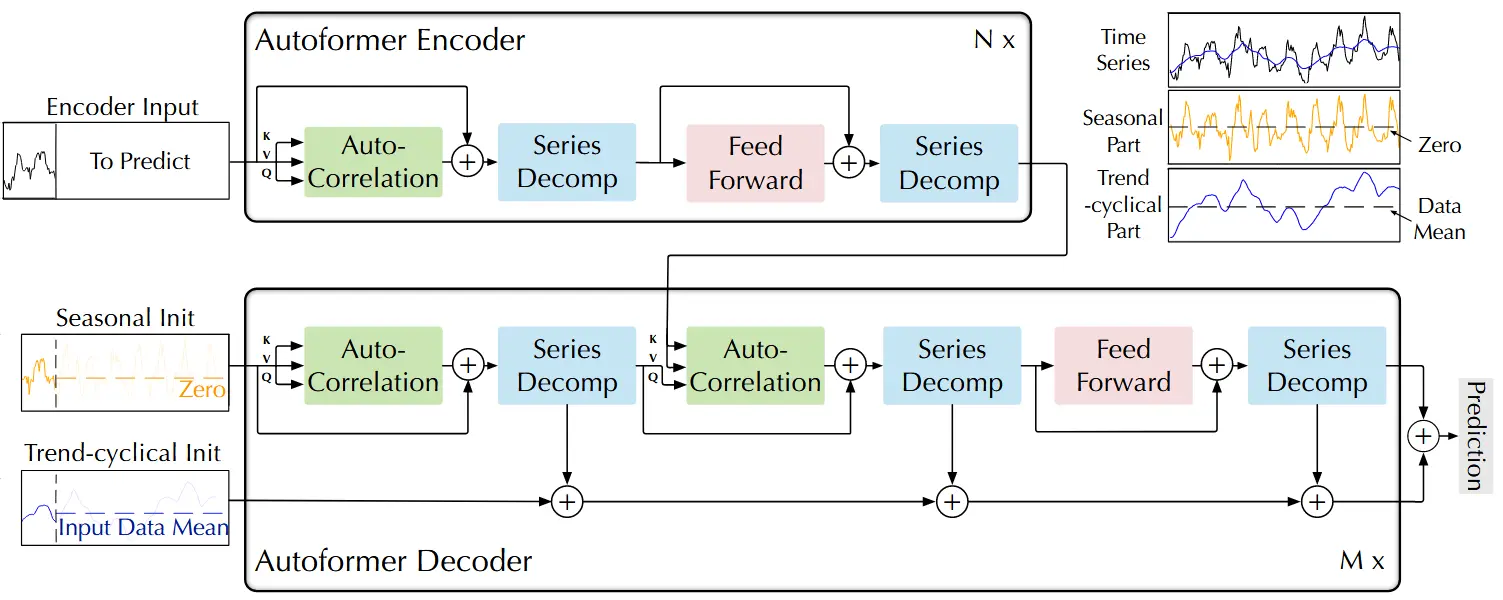
图 1：Autoformer 架构图。编码器通过序列分解模块（图中蓝色模块）去除长期趋势-周期部分，专注于建模季节性模式。解码器则逐步累加从隐藏变量中提取的趋势成分。此外，编码器的历史季节信息通过编码器-解码器自相关机制（图中解码器中央的绿色模块）被有效利用，帮助提升预测精度。

5.4 分解架构（Decomposition Architecture）

我们对传统的 Transformer 进行了改造，构建为一个深度分解架构（如图 1 所示），该架构包括以下组件：内部序列分解模块（series decomposition block）、自相关机制（Auto-Correlation mechanism），以及对应的编码器和解码器结构。

5.4.1 序列分解模块

为了适应长期预测中复杂的时间模式，我们引入了序列分解思想（Series decomposition block），将序列划分为：

• 趋势-周期部分（trend-cyclical part）：反映长期变化趋势；
• 季节性部分（seasonal part）：反映周期性波动。

这两部分分别对应于时间序列的长期演化和短期周期性。然而，由于未来尚未发生，直接对未来序列进行显式分解是不现实的。为解决这一问题，我们将序列分解模块嵌入为 Autoformer 的内部运算单元，用于渐进式地从中间预测变量中提取长期平稳趋势。具体而言，我们引入滑动平均（moving average） 操作来平滑周期波动并突出长期趋势。对于长度为 $L$、维度为 $d$ 的输入序列 $\mathcal{X} \in \mathbb{R}^{L \times d}$，其分解过程如下：

$$\mathcal{X}_t = \text{AvgPool}(\text{Padding}(\mathcal{X}))$$

$$\mathcal{X}_s = \mathcal{X} - \mathcal{X}_t$$

其中：

• $\mathcal{X}_t$ 表示提取出的趋势-周期成分；
• $\mathcal{X}_s$ 表示剩余的季节性成分；
• 滑动平均采用 $\text{AvgPool}(·)$，并通过 Padding 保持序列长度不变。 我们将上述操作简记为：

$$\mathcal{X}_s, \mathcal{X}_t = \text{SeriesDecomp}(\mathcal{X})$$

这个分解过程被用作模型的内部基本构件，在编码器和解码器中被多次调用。

5.5 模型输入（Model inputs）

编码器部分的输入为过去 $I$ 个时间步的数据，即：

$$\mathcal{X}_{\text{en}} \in \mathbb{R}^{I \times d}$$

作为一个分解架构（见图 1），Autoformer 解码器的输入包含两个部分：

• 季节性部分：$\mathcal{X}_{\text{des}} \in \mathbb{R}^{(\frac{I}{2} + O) \times d}$
• 趋势-周期部分：$\mathcal{X}_{\text{det}} \in \mathbb{R}^{(\frac{I}{2} + O) \times d}$

每个输入初始化由两个部分组成：

1. 从编码器输入 $\mathcal{X}_{\text{en}}$ 的后半部分（长度为 $\frac{I}{2}$）中分解出的成分，用于提供最近的历史信息；
2. 长度为 $O$ 的占位符，用标量填充。 其计算过程如下所示：

$$\mathcal{X}_{\text{ens}},\ \mathcal{X}_{\text{ent}} = \text{SeriesDecomp}(\mathcal{X}_{\text{en}}[\frac{I}{2} : I])$$

$$\mathcal{X}_{\text{des}} = \text{Concat}(\mathcal{X}_{\text{ens}},\ \mathcal{X}_0)$$

$$\mathcal{X}_{\text{det}} = \text{Concat}(\mathcal{X}_{\text{ent}},\ \mathcal{X}_{\text{Mean}})$$

其中：

• $\mathcal{X}_{\text{ens}},\ \mathcal{X}_{\text{ent}} \in \mathbb{R}^{\frac{I}{2} \times d}$ 分别表示编码器输入的季节性成分和趋势-周期成分；
• $\mathcal{X}_0,\ \mathcal{X}_{\text{Mean}} \in \mathbb{R}^{O \times d}$ 分别为长度为 $O$ 的占位张量，前者填充为 0，后者填充为 $\mathcal{X}_{\text{en}}$ 的均值。

这样的设计使解码器具备对最近历史趋势的感知能力，并提供预测目标长度的占位结构，用于后续的动态推理和迭代更新。

5.6 编码器（Encoder）

如图 1 所示，编码器的主要功能是建模季节性成分（seasonal part）。编码器输出的是包含历史季节信息的特征，这些信息将作为跨层信息（cross information） 传递给解码器，用于进一步优化预测结果。 假设编码器包含 $N$ 层，第 $l$ 层的整体计算过程可表示为：

$$\mathcal{X}_{\text{en}}^l = \text{Encoder}(\mathcal{X}_{\text{en}}^{l-1})$$

其具体计算步骤如下：

$$\mathcal{S}_{\text{en}, -}^{l,1} = \text{SeriesDecomp}\left( \text{Auto-Correlation}(\mathcal{X}_{\text{en}}^{l-1}) + \mathcal{X}_{\text{en}}^{l-1} \right)$$

$$\mathcal{S}_{\text{en}, -}^{l,2} = \text{SeriesDecomp}\left( \text{FeedForward}(\mathcal{S}_{\text{en}}^{l,1}) + \mathcal{S}_{\text{en}}^{l,1} \right) \tag{3}$$

其中符号 “−” 表示被剔除的趋势成分。第 $l$ 层的最终输出定义为：

$$\mathcal{X}_{\text{en}}^l = \mathcal{S}_{\text{en}}^{l,2},\quad l \in \{1, \dots, N\}$$

而初始输入 $\mathcal{X}_{\text{en}}^0$ 则是对原始输入序列 $\mathcal{X}_{\text{en}}$ 进行嵌入后的结果。其中 $\mathcal{S}_{\text{en}}^{l,i}$，$i \in \{1, 2\}$，表示在第 $l$ 层中，第 $i$ 次分解操作后提取出的季节性分量。接下来的章节将详细介绍 Auto-Correlation(·) 机制，它可以无缝替代传统的自注意力机制。

5.7 解码器（Decoder）

解码器包含两个部分：一是用于趋势-周期成分的累加结构，二是用于季节性成分的堆叠式 Auto-Correlation（自相关）机制（见图 1）。每一层解码器包含两个自相关模块：

• 内部自相关（inner Auto-Correlation），用于细化当前层的预测；
• 编码器-解码器自相关（encoder-decoder Auto-Correlation），用于利用编码器提供的历史季节信息。

值得注意的是，Autoformer 能够在解码过程中从中间隐藏变量中提取潜在的趋势信息，从而逐步细化趋势预测，并消除干扰成分，以便更有效地通过自相关机制发现周期性依赖关系。假设解码器包含 $M$ 层，且来自编码器的隐变量为 $\mathcal{X}_{\text{en}}^N$，第 $l$ 层解码器的整体表达为：

$$\mathcal{X}_{\text{de}}^l = \text{Decoder}(\mathcal{X}_{\text{de}}^{l-1},\ \mathcal{X}_{\text{en}}^N)$$

具体计算过程如下：

$$\mathcal{S}_{\text{de}}^{l,1},\ \mathcal{T}_{\text{de}}^{l,1} = \text{SeriesDecomp} \left( \text{Auto-Correlation}(\mathcal{X}_{\text{de}}^{l-1}) + \mathcal{X}_{\text{de}}^{l-1} \right)$$

$$\mathcal{S}_{\text{de}}^{l,2},\ \mathcal{T}_{\text{de}}^{l,2} = \text{SeriesDecomp} \left( \text{Auto-Correlation}(\mathcal{S}_{\text{de}}^{l,1},\ \mathcal{X}_{\text{en}}^N) + \mathcal{S}_{\text{de}}^{l,1} \right)$$

$$\mathcal{S}_{\text{de}}^{l,3},\ \mathcal{T}_{\text{de}}^{l,3} = \text{SeriesDecomp} \left( \text{FeedForward}(\mathcal{S}_{\text{de}}^{l,2}) + \mathcal{S}_{\text{de}}^{l,2} \right)$$

$$\mathcal{T}_{\text{de}}^l = \mathcal{T}_{\text{de}}^{l-1} + W_{l,1} * \mathcal{T}_{\text{de}}^{l,1} + W_{l,2} * \mathcal{T}_{\text{de}}^{l,2} + W_{l,3} * \mathcal{T}_{\text{de}}^{l,3} \tag{4}$$

其中：

• $\mathcal{X}_{\text{de}}^l = \mathcal{S}_{\text{de}}^{l,3}$ 表示第 $l$ 层解码器的输出，$l \in \{1, \dots, M\}$；
• 初始输入 $\mathcal{X}_{\text{de}}^0$ 是由 $\mathcal{X}_{\text{des}}$ 嵌入而得；
• 初始趋势累加值为 $\mathcal{T}_{\text{de}}^0 = \mathcal{X}_{\text{det}}$；
• $\mathcal{S}_{\text{de}}^{l,i}$、$\mathcal{T}_{\text{de}}^{l,i}$，$i \in \{1, 2, 3\}$ 分别表示第 $l$ 层第 $i$ 个序列分解模块得到的季节性与趋势-周期性部分；
• $W_{l,i}$ 是用于映射趋势部分的投影矩阵。

解码器的这种设计使 Autoformer 能够在每一层中逐步加强趋势建模，同时保留高质量的周期性建模能力。最终的预测结果是两个经过细化的分解分量的和，表示为：

$$\mathcal{W}_S * \mathcal{X}_{\text{de}}^M + \mathcal{T}_{\text{de}}^M$$

其中，$\mathcal{W}_S$ 是将解码器最后一层输出的季节性成分 $\mathcal{X}_{\text{de}}^M$ 映射到目标维度的投影矩阵。

5.8 自相关机制

如图 2 所示，提出了一种基于序列级连接（series-wise connections） 的自相关机制（Auto-Correlation Mechanism），用于提升信息利用率。该机制通过计算时间序列的自相关性，挖掘出基于周期的依赖关系（period-based dependencies），并通过时延聚合（time delay aggregation） 方式将相似的子序列聚合在一起。

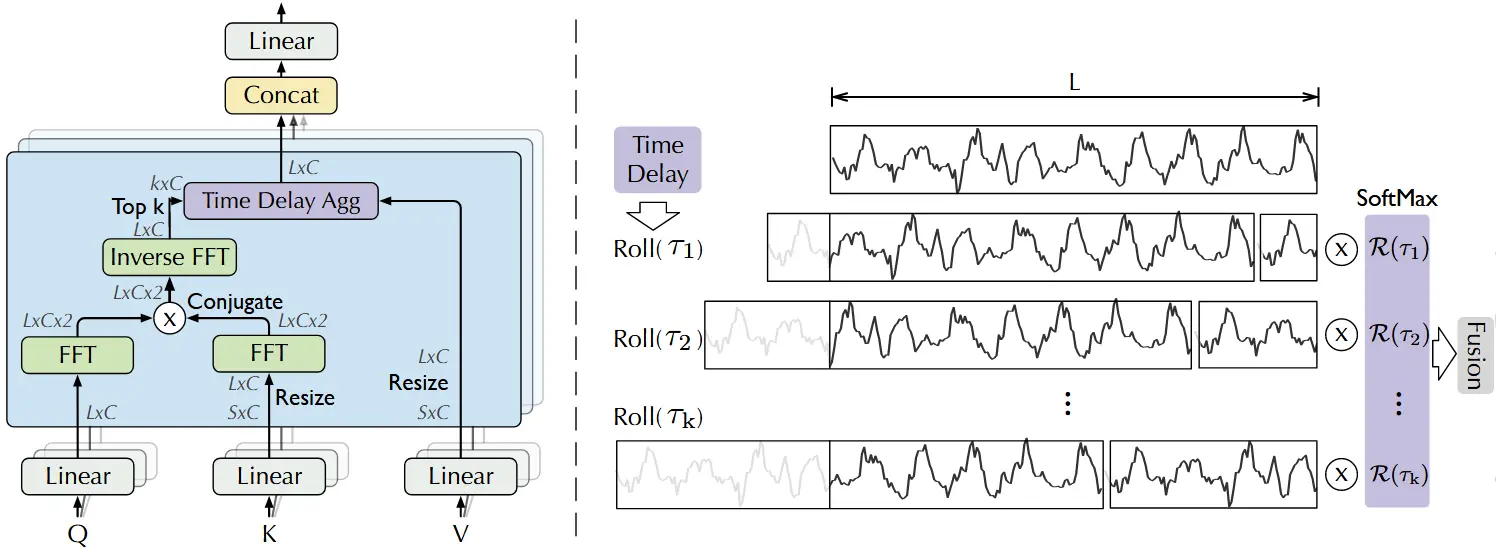
图 2：Auto-Correlation（左）与 Time Delay Aggregation（右）我们利用快速傅里叶变换（FFT）计算自相关函数 $R(\tau)$，以衡量时间序列中不同时间滞后下的相似性。随后，系统会根据选定的滞后 $\tau$ 将相似的子过程对齐到同一索引位置，并通过对应的 $R(\tau)$ 权重进行聚合，从而实现周期性结构的高效建模。

5.8.1 基于周期的依赖关系（Period-based dependencies）

我们观察到，在不同时期中处于相同相位位置的子序列通常具有相似的动态过程。 受到随机过程理论的启发，对于一个离散时间序列过程 $\{X_t\}$，我们可以使用以下公式计算其自相关函数：

$$\mathcal{R}_{XX}(\tau) = \lim_{L \to \infty} \frac{1}{L} \sum_{t=1}^{L} X_t X_{t - \tau} \tag{5}$$

该自相关函数 $\mathcal{R}_{XX}(\tau)$ 表示原始序列 $\{X_t\}$ 与其滞后序列 $\{X_{t - \tau}\}$ 之间的时延相似度。如图 2 所示，我们使用自相关值 $\mathcal{R}(\tau)$ 作为估计周期长度 $\tau$ 的非归一化置信度，然后选取置信度最高的 $k$ 个周期长度 $\tau_1, \dots, \tau_k$。最终，基于这些估计周期得到的周期性依赖结构，可以根据各自的自相关值进行加权聚合。

5.8.2 更详细的解释“基于周期的依赖关系（Period-based dependencies）”

什么是“基于周期的依赖关系”？

在时间序列中，比如温度、销售量、电力负荷等数据，很多现象都是周期性的 —— 每天、每周、每年都有相似的模式。比如：你可以想象每天早上 8 点上班高峰的交通流量和前一天早上 8 点是相似的。这个现象说明：处于不同周期中“相同时间点”的子序列，往往有类似的模式。这就叫做：周期性依赖（period-based dependencies）。

为什么要用自相关函数（Autocorrelation）？

我们希望找到：时间序列中，哪些“时间差（滞后）”最有可能形成周期性。 比如我们观察销售数据，发现每隔 7 天模式会重复——这说明周期是 7 天。那我们怎么找出这个“7天”？ 我们用的是这个公式：

$$\mathcal{R}_{XX}(\tau) = \lim_{L \to \infty} \frac{1}{L} \sum_{t=1}^{L} X_t X_{t - \tau}$$

解释一下这个式子：

• $X_t$：时间点 $t$ 的数值；
• $X_{t - \tau}$：时间点 $t - \tau$ 的数值；
• 把 $X_t$ 和它前面 $\tau$ 个时间步的值相乘并求和，就是看它们之间是否“同步”；
• 如果这个值很大，说明当前和过去 $\tau$ 步前的模式很相似。

这就叫自相关（autocorrelation）：它告诉你在滞后（delay）$\tau$ 情况下，序列有多像自己。

怎么用自相关找出“周期”？

1. 对每一个 $\tau \in \{1, 2, ..., L\}$，都计算出 $\mathcal{R}_{XX}(\tau)$，看哪些滞后值自相关最大；
2. 找出前 $k$ 个最大的自相关值对应的 $\tau$：也就是最有可能的周期长度；
3. 用这些滞后（周期长度）对齐历史数据中相同“相位位置”的子序列（比如一周前的同一时间），进行加权聚合；
4. 权重就是这些 $\mathcal{R}_{XX}(\tau)$ 的值——越像，权重越大。

5.8.3 时延聚合（Time delay aggregation）

基于周期的依赖关系将估计周期中的子序列连接起来。为此，我们提出时延聚合模块（time delay aggregation block）（见图 2），该模块可以根据选定的时延 $\tau_1, \dots, \tau_k$ 对序列进行“卷动”（roll），从而对齐这些处于相同相位位置的相似子序列。

这一过程不同于自注意力机制中的点乘聚合，它可以基于周期性对整段子序列进行聚合。最后，我们使用 softmax 归一化的置信度对子序列进行加权平均。对于单头注意力情况下，设长度为 $L$ 的时间序列经过投影后得到查询（query）$\mathcal{Q}$、键（key）$\mathcal{K}$、值（value）$\mathcal{V}$，则该机制的计算过程如下：

$$\tau_1, \dots, \tau_k = \arg\operatorname{Topk}_{\tau \in \{1, \dots, L\}} \left( \mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau) \right)$$

$$\widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}(\tau_1), \dots, \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}(\tau_k) = \operatorname{SoftMax} \left( \mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau_1), \dots, \mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau_k) \right)$$

$$\text{Auto-Correlation}(\mathcal{Q}, \mathcal{K}, \mathcal{V}) = \sum_{i=1}^k \operatorname{Roll}(\mathcal{V}, \tau_i)\ \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}(\tau_i) \tag{6}$$

其中：

• $\operatorname{argTopk}(\cdot)$ 用于选择最大的 $k = \lfloor c \cdot \log L \rfloor$ 个自相关项，$c$ 是超参数；
• $\mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau)$ 是序列 $\mathcal{Q}$ 和 $\mathcal{K}$ 之间滞后为 $\tau$ 时的自相关；
• $\operatorname{Roll}(\mathcal{V}, \tau)$ 表示将值序列向右移动 $\tau$ 个时间步，超出部分补到末尾（循环）；
• 在编码器-解码器自相关中，$\mathcal{K}$ 和 $\mathcal{V}$ 来自编码器输出 $\mathcal{X}_{\text{en}}^N$，会被调整为预测长度 $O$，而 $\mathcal{Q}$ 来自解码器的前一层。

多头版本（Multi-head version）

在 Autoformer 中，使用了多头机制。若总通道数为 $d_{\text{model}}$，头数为 $h$，则第 $i$ 个头的查询、键、值为：

$$\mathcal{Q}_i,\ \mathcal{K}_i,\ \mathcal{V}_i \in \mathbb{R}^{L \times \frac{d_{\text{model}}}{h}},\quad i \in \{1, \dots, h\}$$

其多头计算过程为：

$$\text{MultiHead}(\mathcal{Q}, \mathcal{K}, \mathcal{V}) = \mathcal{W}_{\text{output}} * \text{Concat}(\text{head}_1, \dots, \text{head}_h) \tag{7}$$

其中每个头的计算为：

$$\text{head}_i = \text{Auto-Correlation}(\mathcal{Q}_i, \mathcal{K}_i, \mathcal{V}_i)$$

这一设计使得 Autoformer 能够在子序列级别进行并行的周期性聚合操作，从而增强模型的表示能力和效率。

5.8.4 更详细解释"时延聚合（Time delay aggregation）"

背景回顾：我们为什么需要聚合？

我们已经通过 自相关机制 找到了几个最可能的周期长度（也就是几个滞后值）：

$$\tau_1, \tau_2, \dots, \tau_k$$

这意味着，当前时间点的行为，可能和时间序列中滞后 $\tau_1$、$\tau_2$、... 的位置非常相似。所以，我们的目标就是： 从时间序列中把这些“滞后位置”的内容提取出来，对齐（roll）到当前时间点的位置，并进行聚合，帮助当前时间点做出更准确的预测。

什么是 Roll 操作？

Roll 是一个类似“向后平移”的操作。比如对于值序列：

原始序列： [A, B, C, D, E]
Roll(τ=2)：[D, E, A, B, C]

你可以把它想成：我们把过去的数据“滑”过来，让它和当前时间对齐。对于每一个滞后 $\tau_i$，我们都对值序列 $\mathcal{V}$ 做一次 roll 操作。

Time Delay Aggregation 怎么工作？

我们有：

• $\mathcal{V}$：值序列（从 encoder 或 decoder 中得到的隐藏表示）；
• $\tau_1, \dots, \tau_k$：自相关函数选出的滞后；
• $\widehat{\mathcal{R}}(\tau_i)$：每个滞后的置信权重（softmax 归一化后）； 那么整个聚合过程是：

$$\text{Auto-Correlation}(\mathcal{Q}, \mathcal{K}, \mathcal{V}) = \sum_{i=1}^k \operatorname{Roll}(\mathcal{V},\ \tau_i)\ \cdot\ \widehat{\mathcal{R}}(\tau_i)$$

解释这一步：

1. 对每个 $\tau_i$，我们将值序列 $\mathcal{V}$ roll（平移）$\tau_i$ 个位置；
2. 这样，相似的子序列就会被移动到当前时间点的位置；
3. 然后用对应的自相关权重 $\widehat{\mathcal{R}}(\tau_i)$ 进行加权；
4. 最后把所有 roll 的结果加起来，得到当前时间点的输出。

这就是 Time Delay Aggregation：它不是点与点之间做注意力加权，而是一整段子序列之间的周期性聚合。

和 Self-Attention 的区别？

Self-Attention	Auto-Correlation（Time Delay Aggregation）
点与点之间的权重计算	子序列与子序列之间的周期对齐与聚合
注意力是点乘计算得到	依赖于 FFT 计算的自相关函数
聚合方式是点乘加权	聚合方式是 roll 对齐 + 加权求和
无结构地学习注意力权重	明确利用周期性结构进行聚合

举个例子

假设你在预测今天的电力负荷，模型通过自相关发现：

• 上周同一时段（$\tau = 168$ 小时）非常相似；
• 昨天同一时段（$\tau = 24$ 小时）也有一定参考价值。

那么：

• 模型会把“上周”和“昨天”的值序列 roll 到当前时间；
• 然后按它们的相似度（自相关强度）加权；
• 最终得到当前时刻的一个更准确的表示（用于预测）。

5.8.5 高效计算（Efficient computation）

对于基于周期的依赖关系而言，这些依赖通常指向处于周期结构中相同相位位置的子过程，因此它们在本质上是稀疏的。在实际实现中，我们选择最可能的几个时延（delays）来避免相位混淆。由于我们聚合的是 $\mathcal{O}(\log L)$ 个长度为 $L$ 的子序列，因此公式 (6) 和 (7) 的总计算复杂度为：

$$\mathcal{O}(L \log L)$$

为高效计算自相关项 $\mathcal{R}_{XX}(\tau)$，我们可基于 Wiener–Khinchin 定理使用**快速傅里叶变换（FFT）**进行处理：

$$\mathcal{S}_{XX}(f) = \mathcal{F}(X_t)\ \mathcal{F}^*(X_t) = \int_{-\infty}^{\infty} X_t e^{-i2\pi t f} dt \cdot \int_{-\infty}^{\infty} X_t e^{-i2\pi t f} dt$$

$$\mathcal{R}_{XX}(\tau) = \mathcal{F}^{-1}(\mathcal{S}_{XX}(f)) = \int_{-\infty}^{\infty} \mathcal{S}_{XX}(f) e^{i2\pi f \tau} df \tag{8}$$

其中：

• $\tau \in \{1, \dots, L\}$；
• $\mathcal{F}$ 表示 FFT，$\mathcal{F}^{-1}$ 是其逆变换；
• 星号（$*$）表示共轭操作；
• $\mathcal{S}_{XX}(f)$ 是频域下的功率谱。 注意：对所有可能的滞后（lag）计算自相关序列只需进行一次 FFT，即可高效完成。因此，Auto-Correlation 机制可实现 $\mathcal{O}(L \log L)$ 的计算复杂度。

[!NOTE] 可以看这个视频了解傅里叶变换相关知识。 https://www.bilibili.com/video/BV1A4411Y7vj/ (opens new window)

5.8.6 更详细的解释“高效计算（Efficient computation）”

目标回顾：我们要干嘛？

在 Autoformer 中，我们要计算一个序列的 自相关函数 $\mathcal{R}_{XX}(\tau)$ ——也就是： “当前序列”和“它自己向前或向后平移 $\tau$ 个时间点”之间有多相似？我们要对很多个滞后 $\tau = 1, 2, ..., L$ 都算一次这个相似度。

标准计算方式是这样：

$$\mathcal{R}_{XX}(\tau) = \frac{1}{L} \sum_{t=1}^{L} X_t \cdot X_{t - \tau}$$

这在时间上是 $\mathcal{O}(L^2)$，如果序列很长，比如上千上万个时间点，光计算这个就要花很多时间！

怎么提速？用傅里叶变换（FFT）

我们用Wiener–Khinchin 定理告诉我们一个非常强大的事实：“一个序列的 自相关函数，其实就是它的频域功率谱（spectrum）做反变换”。数学上是：

$$\mathcal{S}_{XX}(f) = \mathcal{F}(X_t) \cdot \mathcal{F}^*(X_t)$$

• $\mathcal{F}(X_t)$ 是序列的 快速傅里叶变换（FFT）；
• $\mathcal{F}^*(X_t)$ 是它的复共轭；
• $\mathcal{S}_{XX}(f)$ 是功率谱（frequency domain 的表示）；

然后我们再做一次 逆傅里叶变换（IFFT）：

$$\mathcal{R}_{XX}(\tau) = \mathcal{F}^{-1}(\mathcal{S}_{XX}(f))$$

这样我们就得到了所有滞后 $\tau \in \{1, ..., L\}$ 的自相关值！

效果：

• 快速傅里叶变换和它的逆变换都是 $\mathcal{O}(L \log L)$；
• 比原始的 $\mathcal{O}(L^2)$ 快太多了！

为什么说 Auto-Correlation 是稀疏的？

因为我们并不需要用所有的滞后 $\tau \in \{1, \dots, L\}$ 去聚合序列，只需要从中选出最相关的前 $k \approx \log L$ 个滞后（用 softmax 归一化后作为权重）即可。也就是说，我们只需要聚合 $\mathcal{O}(\log L)$ 个子序列，不是所有的！

这就说明了：Autoformer 的时间依赖是“周期结构中稀疏连接”的，而不是所有时间点都连。

最终复杂度是多少？

• 用 FFT 算所有滞后的自相关值：$\mathcal{O}(L \log L)$
• 聚合前 $k = \log L$ 个滞后对应的子序列（每个长度是 $L$）：也仍是 $\mathcal{O}(L \log L)$

所以，最终整个 Auto-Correlation 机制的复杂度是：$\mathcal{O}(L \log L)$ ，相比原始 Transformer 的 $\mathcal{O}(L^2)$ 自注意力机制高效得多！

总结一句话：

Autoformer 用 FFT + 稀疏周期聚合，在保持预测精度的同时，实现了比自注意力机制更快更省内存的计算方式。它不是“近似”，而是利用时间序列的周期结构进行高效建模。

5.9 Auto-Correlation 与 Self-Attention 的对比

与点对点（point-wise）的自注意力机制不同，Auto-Correlation 提供的是序列级（series-wise）连接（如图 3 所示）。具体来说，在建模时间依赖关系时，Auto-Correlation 依据周期性来发现子序列之间的相关性；而自注意力机制只关注离散点之间的相似性。

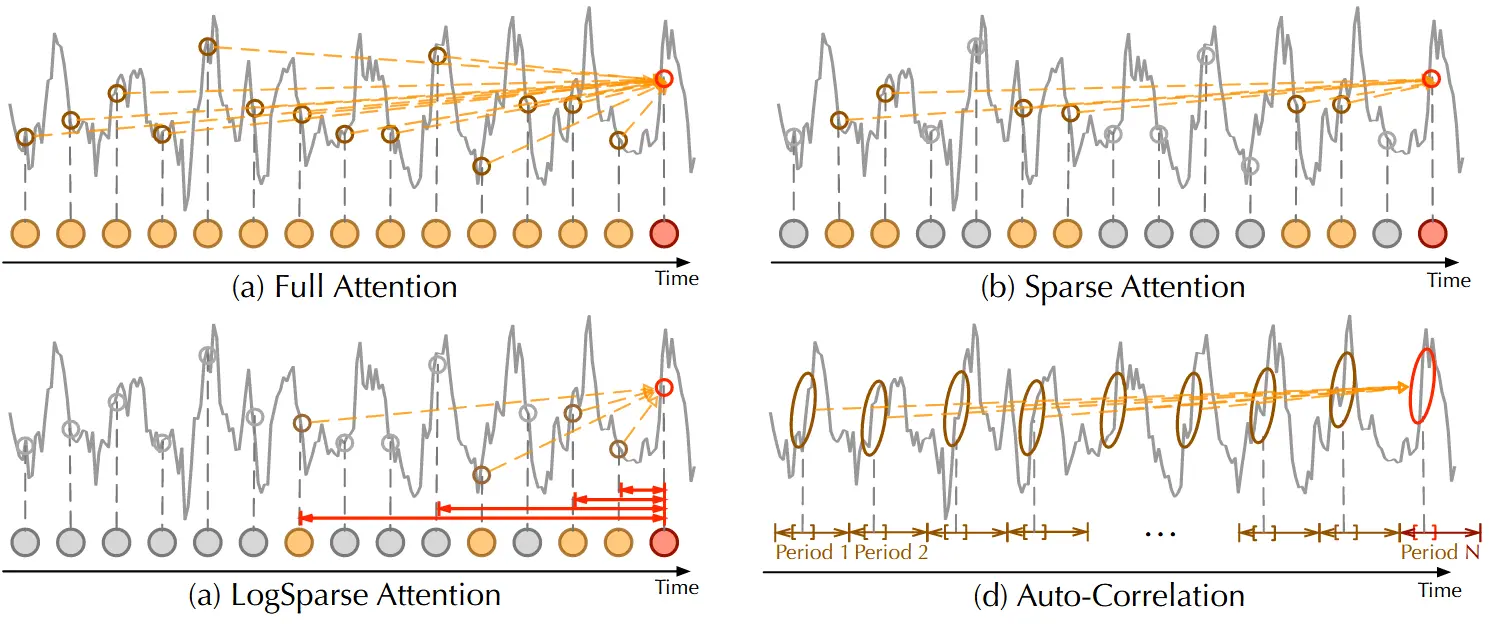
图 3：Auto-Correlation 与自注意力机制家族的对比：

• (a) Full Attention：采用全连接方式，计算所有时间点之间的关系。
• (b) Sparse Attention：根据预设的相似性指标选择部分时间点进行连接。
• (c) LogSparse Attention：按照指数间隔选择时间点，从而降低计算复杂度。
• (d) Auto-Correlation：专注于不同周期中处于相同相位的子序列之间的连接，以捕捉周期性依赖关系。 相比之下，Auto-Correlation 是一种基于周期结构的子序列级连接机制，区别于传统自注意力中的点对点建模方式。

尽管某些自注意力机制（如 Informer、LogTrans）也考虑局部信息，但它们的目标仍是提升点级连接的选择质量，并未在结构上突破点级建模方式。在信息聚合方面，Auto-Correlation 采用时延聚合（time delay aggregation），将来自相同周期相位的子序列进行融合；而自注意力机制通过点乘的方式对选中位置进行加权。

因此，得益于其固有的稀疏性与子序列级表示能力，Auto-Correlation 在计算效率与信息利用率之间实现了更好的平衡，具备同时提升两者的潜力。

6 实验细节

我们的方法使用 L2 损失函数进行训练，并采用 ADAM 优化器，初始学习率设为 $10^{-4}$。批量大小（batch size）为 32，训练过程采用早停策略，在 10 个 epoch 内若无改进则终止。所有实验均重复三次以提高可靠性，使用 PyTorch 框架实现，并在一块 NVIDIA TITAN RTX 24GB GPU 上进行训练。Auto-Correlation 模块中的超参数 $c$ 设置在 1 到 3 之间，以权衡性能与效率之间的平衡。关于标准差与敏感性分析的更多内容，请参见附录 E 和 B。在模型结构上，Autoformer 使用 2 层编码器 和 1 层解码器。